Projected changes in precipitation-based indices for impact models

5.2.4. Projected changes in precipitation-based indices for impact models#

Production date: 29-05-2024

Produced by: CMCC foundation - Euro-Mediterranean Center on Climate Change. Albert Martinez Boti.

🌍 Use case: Verification of precipitation indices used as proxies for rainfall erosivity in Europe under future climate scenarios.#

❓ Quality assessment question#

What are the projected future changes and associated uncertainties of precipitation-based indices in Europe?

Soil erosion stands as one of the primary environmental concerns in Europe [1]. Its accelerated occurrence can precipitate a decline in ecosystem stability, land productivity, and overall land degradation, resulting in diminished income for farmers [2]. This notebook is designed to evaluate the uncertainty in future projections of a specific set of models from CORDEX Regional Climate Models (RCMs) by considering the ensemble inter-model spread of projected changes. These selected rainfall indicators are recognised as valuable proxies for rainfall erosivity, a factor directly linked to empirical calculations of soil loss, as outlined in an application available through the old CDS platform (dataset documentation) The five precipitation-based indices used here are calculated using the icclim package, them being:

Spell length of days with precipitation greater than 1 mm (also known as “Maximum consecutive wet days” - “CWD”)
Number of heavy precipitation days (Precip >= 20mm - “R20mm”)
Number of wet days (Precip >= 1mm - “RR1”)
Maximum 1-day total precipitation (“RX1day”)
Maximum 5-day total precipitation (“RX5day”).

Within this notebook, these calculations are performed over the temporal aggregation of DJF and for the future period spanning from 2015 to 2099, following the Representative Concentration Pathway RCP 8.5. It is important to note that the results presented here pertain to a specific subset of the CORDEX ensemble and may not be generalisable to the entire dataset. Also note that a separate assessment examines the representation of climatology and trends of these indices for the same models during the historical period (1971-2000).

📢 Quality assessment statement#

These are the key outcomes of this assessment

For the selected subset of models, future projections suggest diversity on the sign of the trend of precipitation-based indices for the DJF aggregation depending on the index selection and the region under consideration.
The spatially-averaged values displayed by boxplots illustrate the diversity of outcomes, emphasising the importance of regional analyses. There is a significant inter-model variability, suggesting uncertainties in future projections. It is essential to note that the interpretation of boxplot results should be approached cautiously, considering the potential distortion of outcomes due to the influence of regions with trends that behave differently.
A larger GCM-RCM matrix should be considered when addressing specific cases to enhance the robustness of the analysis and account for uncertainties [3][4].
The outcomes of this notebook are highly dependent on the index and region. Projected changes for RR1, RX1day, and RX5day show similar spatial patterns among the subset of considered models. In contrast, CWD and R20mm exhibit more scattered spatial patterns, and the regions with significant trend signals appear to have large uncertainties (inter-model spread). Results obtained from another assessment of the same indices and temporal aggregation (DJF) for the historical period 1971-2000, which evaluated biases (“CORDEX Climate Projections: evaluating bias in precipitation-based indices for impact models”), should also be taken into consideration. The high uncertainties in both assessments encourage users to bias-correct precipitation-based indices before using them for specific applications [5].
Model agreement on precipitation-based indices projections is lower than on maximum temperature indices. This difference is evident when comparing the results of this assessment with those obtained in “RCM uncertainty in projected changes in extreme temperature indices for the reinsurance sector”

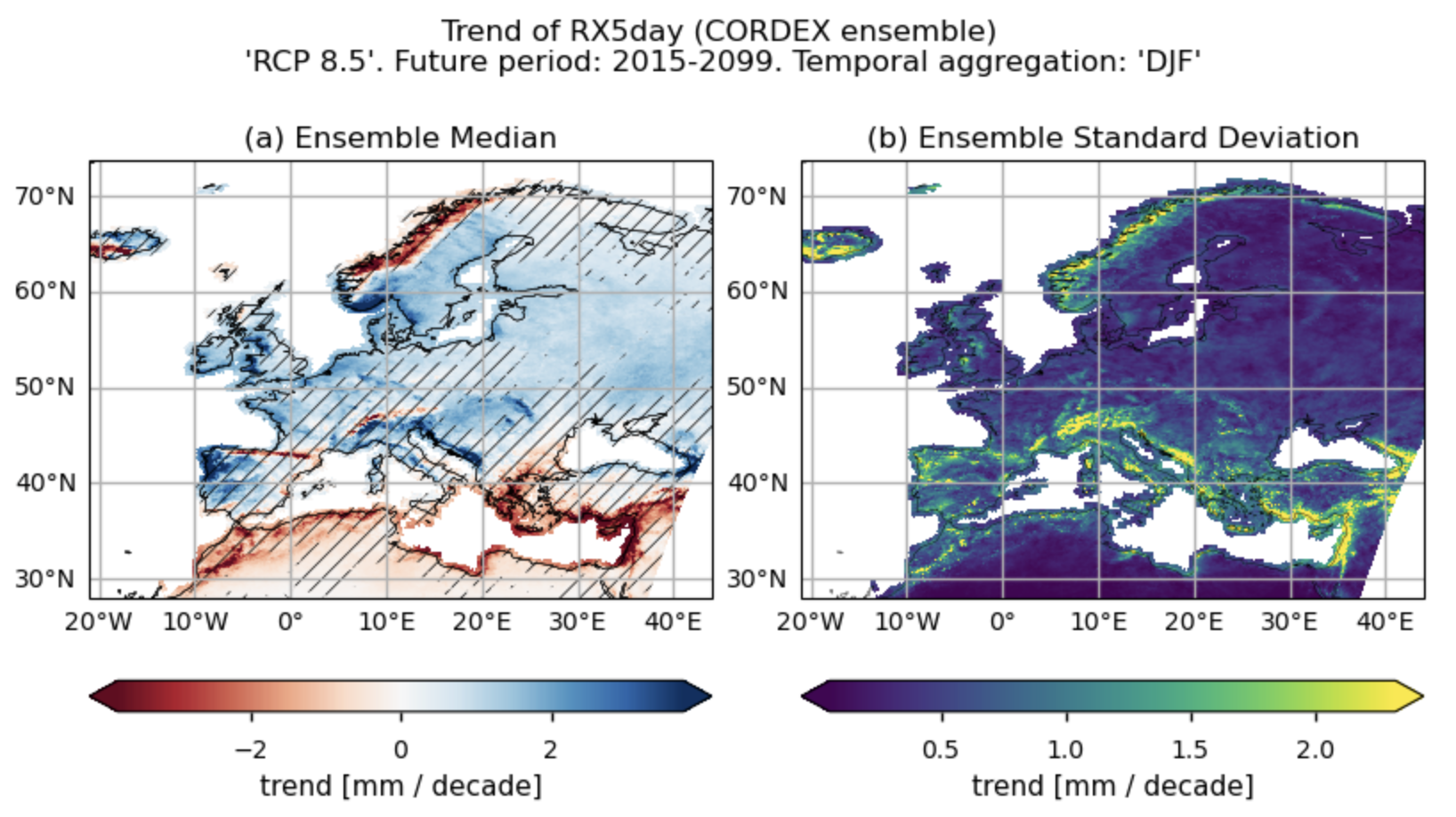
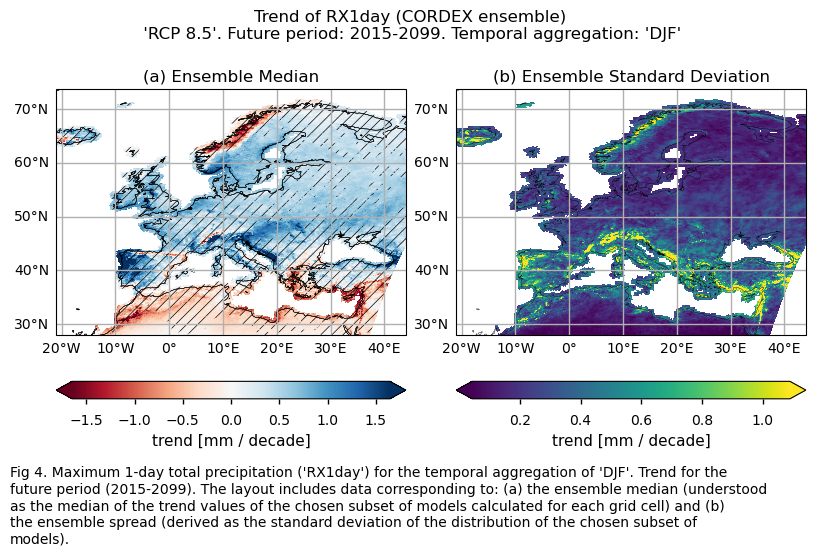
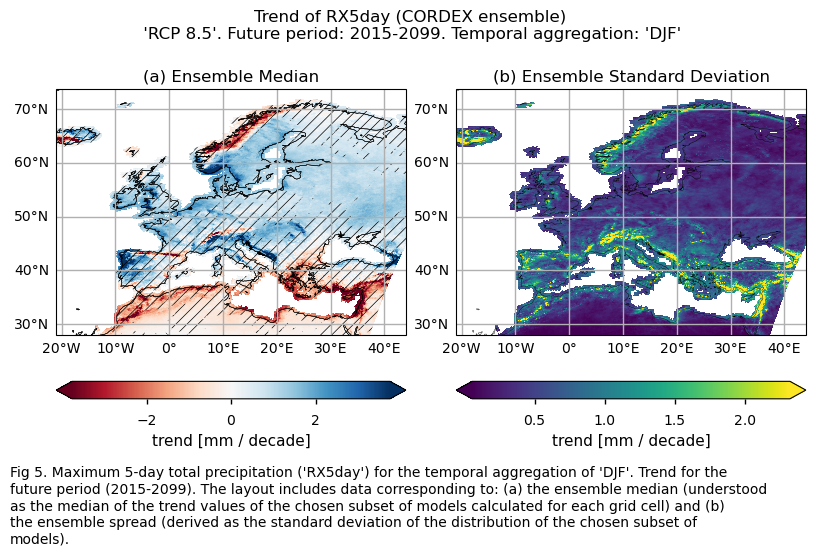
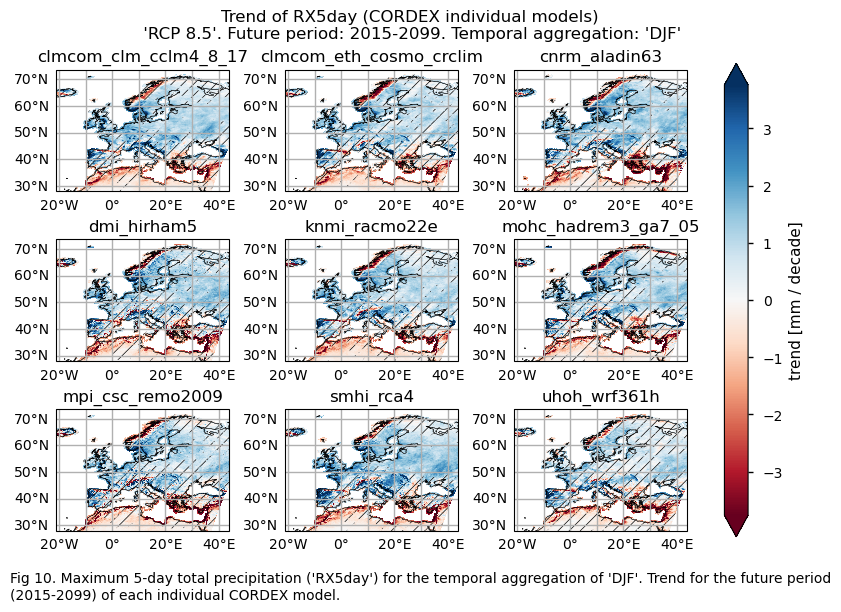
trend_future_RX5day — Fig. 5.2.4.1 Maximum 5-day total precipitation (‘RX5day’) for the temporal aggregation of ‘DJF’. Trend for the future period (2015-2099). The layout includes data corresponding to: (a) the ensemble median (understood as the median of the trend values of the chosen subset of models calculated for each grid cell) and (b) the ensemble spread (derived as the standard deviation of the distribution of the chosen subset of models).#

NOTE on the DJF selection:
It is important to note that using seasonal temporal aggregations offers only partial insights into the dynamics. For more comprehensive results, it is advisable to also consider other seasons and annual aggregations. However, for the sake of efficiency and to avoid making the notebook too heavy, we have opted to prioritise seasonal aggregations.

📋 Methodology#

This notebook offers an assessment of the projected changes and their associated uncertainties using a subset of 9 models from CORDEX. The analysis involves evaluating the ensemble inter-model spread of projected changes using several precipitation-based indices. These indices, calculated over the DJF period for the future period spanning from 2015 to 2099, include:

Spell length of days with precipitation greater than 1 mm (also known as “Maximum consecutive wet days” - “CWD”)
Number of heavy precipitation days (Precip >= 20mm - “R20mm”)
Number of wet days (Precip >= 1mm - “RR1”)
Maximum 1-day total precipitation (“RX1day”)
Maximum 5-day total precipitation (“RX5day”).

In particular, spatial patterns of climate projected trends are examined and displayed for each model individually and for the ensemble median (calculated for each grid cell), alongside the ensemble inter-model spread to account for projected uncertainty. Additionally, spatially-averaged trend values are analysed and presented using box plots to provide an overview of trend behavior across the distribution of the chosen subset of models when averaged across Europe.

The analysis and results follow the next outline:

1. Parameters, requests and functions definition

1.1. Import packages
1.2. Define Parameters
1.3. Define models
1.4. Define land-sea mask request
1.5. Define model requests
1.6. Functions to cache

2. Downloading and processing

2.1. Download and transform the regridding model
2.2. Download and transform models
2.3. Apply land-sea mask, change attributes and cut the region to show

3. Plot and describe results

3.1. Define plotting functions
3.2. Plot ensemble maps
3.3. Plot model maps
3.4. Boxplots of the future trend
3.5. Results summary and discussion

📈 Analysis and results#

1. Parameters, requests and functions definition#

1.1. Import packages#

1.2. Define Parameters#

In the “Define Parameters” section, various customisable options for the notebook are specified. Most of the parameters chosen are the same as those used in another assessment (“CORDEX Climate Projections: evaluating bias in precipitation-based indices for impact models”), being them:

The initial and ending year used for the future projections period can be specified by changing the parametes future_slice (2015-2099 is chosen for consistency between CORDEX and CMIP6).
The timeseries set the temporal aggregation. For instance, selecting “DJF” implies considering only the winter season.
collection_id provides the choice between Global Climate Models CMIP6 or Regional Climate Models CORDEX. Although the code allows choosing between CMIP6 or CORDEX, the example provided in this notebook deals with CORDEX RCMs.
area allows specifying the geographical domain of interest.
The interpolation_method parameter allows selecting the interpolation method when regridding is performed over the indices.
The chunk selection allows the user to define if dividing into chunks when downloading the data on their local machine. Although it does not significantly affect the analysis, it is recommended to keep the default value for optimal performance.

1.3. Define models#

he following climate analyses are performed considering a subset of GCMs from CMIP6. Models names are listed in the parameters below. Some variable-dependent parameters are also selected, as the index_names parameter, which specifies the precipitation-based indices (‘CWD’, ‘R20mm’, ‘RR1’, ‘RX1day’ and ‘RX5day’ in our case) from the icclim Python package.

When choosing Cordex models, it is crucial to consider the availability of RCMs for the selected GCM and the specified region. The listed RCMs, for instance, are accessible for the GCM “mpi_m_mpi_esm_lr” in the “europe” cordex_domain, and they are the same as those used in another assessment (“CORDEX Climate Projections: evaluating bias in precipitation-based indices for impact models”). To confirm the available combinations, refer to the CORDEX CDS catalogue entry.

Show code cell source

Hide code cell source

models_cordex = (
    "clmcom_clm_cclm4_8_17",
    "clmcom_eth_cosmo_crclim",
    "cnrm_aladin63",
    "dmi_hirham5",
    "knmi_racmo22e",
    "mohc_hadrem3_ga7_05",
    "mpi_csc_remo2009",
    "smhi_rca4",
    "uhoh_wrf361h",
)

match variable:
    case "temperature":
        resample_reduction = "max"
        index_names = ("SU", "TX90p")
        era5_variable = "2m_temperature"
        cordex_variable = "maximum_2m_temperature_in_the_last_24_hours"
        cmip6_variable = "daily_maximum_near_surface_air_temperature"
        models_cmip6 = (
            "access_cm2",
            "awi_cm_1_1_mr",
            "cmcc_esm2",
            "cnrm_cm6_1_hr",
            "ec_earth3_cc",
            "gfdl_esm4",
            "inm_cm5_0",
            "miroc6",
            "mpi_esm1_2_lr",
        )
        # Colormaps
        cmaps="viridis"
        cmaps_trend = cmaps_bias = "RdBu_r"
        #Define dictionaries to use in titles and caption
        long_name = {
            "SU":"Number of summer days",
            "TX90p":"Number of days with daily maximum temperatures exceeding the daily 90th percentile of maximum temperature for a 5-day moving window",
        }
    case "precipitation":
        resample_reduction = "sum"
        index_names = ("CWD", "R20mm", "RR1", "RX1day", "RX5day")
        era5_variable = "total_precipitation"
        cordex_variable = "mean_precipitation_flux"
        cmip6_variable = "precipitation"
        models_cmip6 = (
            "access_cm2",
            "bcc_csm2_mr",
            "cmcc_esm2",
            "cnrm_cm6_1_hr",
            "ec_earth3_cc",
            "gfdl_esm4",
            "inm_cm5_0",
            "miroc6",
            "mpi_esm1_2_lr",
        )
        # Colormaps
        cmaps="Blues"
        cmaps_trend = cmaps_bias = "RdBu"
        #Define dictionaries to use in titles and caption
        long_name = {
            "RX1day": "Maximum 1-day total precipitation",
            "RX5day": "Maximum 5-day total precipitation",
            "RR1":"Number of wet days (Precip >= 1mm)",
            "R20mm":"Number of heavy precipitation days (Precip >= 20mm)",
            "CWD":"Maximum consecutive wet days",
        }
    case _:
        raise NotImplementedError(f"{variable=}")

model_regrid = "gfdl_esm4" if collection_id == "CMIP6" else "clmcom_eth_cosmo_crclim"

1.4. Define land-sea mask request#

Within this notebook, ERA5 will be used to download the land-sea mask when plotting. In this section, we set the required parameters for the cds-api data-request of ERA5 land-sea mask.

1.5. Define model requests#

In this section we set the required parameters for the cds-api data-request.

The get_cordex_years function is employed to choose suitable data chunks for CORDEX data requests.

When Weights = True, spatial weighting is applied for calculations requiring spatial data aggregation. This is particularly relevant for CMIP6 GCMs with regular lon-lat grids that do not consider varying surface extensions at different latitudes. In contrast, CORDEX RCMs, using rotated grids, inherently account for different cell surfaces based on latitude, eliminating the need for a latitude cosine multiplicative factor (Weights = False).

Show code cell source

Hide code cell source

request_cordex = {
    "format": "zip",
    "domain": "europe",
    "horizontal_resolution": "0_11_degree_x_0_11_degree",
    "temporal_resolution": "daily_mean",
    "variable": cordex_variable,
    "gcm_model": "mpi_m_mpi_esm_lr",
    "ensemble_member": "r1i1p1",
}

request_cmip6 = {
    "format": "zip",
    "temporal_resolution": "daily",
    "variable": cmip6_variable,
    "month": [f"{month:02d}" for month in range(1, 13)],
    "day": [f"{day:02d}" for day in range(1, 32)],
    "area": area,
}


def get_cordex_years(
    year_slice,
    timeseries,
    start_years=list(range(1951, 2097, 5)),
    end_years=list(range(1955, 2101, 5)),
):
    start_year = []
    end_year = []
    years = set(
        range(year_slice.start - int(timeseries == "DJF"), year_slice.stop + 1)
    )  # Include D(year-1)
    for start, end in zip(start_years, end_years):
        if years & set(range(start, end + 1)):
            start_year.append(start)
            end_year.append(end)
    return start_year, end_year


def get_cmip6_years(year_slice):
    return [
        str(year)
        for year in range(
            year_slice.start - int(timeseries == "DJF"),  # Include D(year-1)
            year_slice.stop + 1,
        )
    ]


model_requests = {}
if collection_id == "CORDEX":
    for model in models_cordex:
        start_years = [1970 if model in ("smhi_rca4", "uhoh_wrf361h") else 1966] + list(
            range(1971, 2097, 5)
        )
        end_years = [1970] + list(range(1975, 2101, 5))
        # Historical
        if variable == "precipitation":
            requests = []
        else:
            requests = [
                {
                    **request_cordex,
                    "experiment": "historical",
                    "start_year": start_year,
                    "end_year": end_year,
                    "rcm_model": model,
                }
                for start_year, end_year in zip(
                    *get_cordex_years(
                        historical_slice, timeseries, start_years, end_years
                    )
                )
            ]
        # Future
        requests += [
            {
                **request_cordex,
                "experiment": "rcp_8_5",
                "start_year": start_year,
                "end_year": end_year,
                "rcm_model": model,
            }
            for start_year, end_year in zip(
                *get_cordex_years(future_slice, timeseries, start_years, end_years)
            )
        ]
        model_requests[model] = ("projections-cordex-domains-single-levels", requests)
elif collection_id == "CMIP6":
    # Historical
    if variable == "precipitation":
        requests = []
    else:
        requests = download.split_request(
            request_cmip6
            | {"year": get_cmip6_years(historical_slice), "experiment": "historical"},
            chunks=chunks,
        )
    # Future
    requests += download.split_request(
        request_cmip6
        | {"year": get_cmip6_years(future_slice), "experiment": "ssp5_8_5"},
        chunks=chunks,
    )
    for model in models_cmip6:
        model_requests[model] = (
            "projections-cmip6",
            [request | {"model": model} for request in requests],
        )
else:
    raise ValueError(f"{collection_id=}")

request_grid_out = model_requests[model_regrid]

1.6. Functions to cache#

In this section, functions that will be executed in the caching phase are defined. Caching is the process of storing copies of files in a temporary storage location, so that they can be accessed more quickly. This process also checks if the user has already downloaded a file, avoiding redundant downloads.

Functions description:

The select_timeseries function subsets the dataset based on the chosen timeseries parameter.
The compute_indices function utilises the icclim package to calculate the precipitation-based indices.
The compute_trends function employs the Mann-Kendall test for trend calculation.
Finally, the compute_indices_and_trends function calculates the precipitation-based indices for the corresponding temporal aggregation using the compute_indices function, determines the indices mean for the future period (2015-2099), obtain the trends using the compute_trends function, and offers an option for regridding to model_regrid.

Show code cell source

Hide code cell source

def select_timeseries(ds, timeseries, year_slice, index_names):
    if timeseries == "annual":
        return ds.sel(time=slice(str(year_slice.start), str(year_slice.stop)))
    ds=ds.sel(time=slice(f"{year_slice.start-1}-12", f"{year_slice.stop}-11"))
    if "RX5day" in index_names:
        return ds
    return ds.where(ds["time"].dt.season == timeseries, drop=True)  


def compute_indices(
    ds,
    index_names,
    timeseries,
    tmpdir,
    future_slice,
    historical_slice,
):
    labels, datasets = zip(*ds.groupby("time.year"))
    paths = [f"{tmpdir}/{label}.nc" for label in labels]
    datasets = [ds.chunk(-1) for ds in datasets]
    xr.save_mfdataset(datasets, paths)

    ds = xr.open_mfdataset(paths)
    in_files = f"{tmpdir}/rechunked.zarr"
    chunks = {dim: 365 * 4 if dim == "time" else "auto" for dim in ds.dims}
    ds.chunk(chunks).to_zarr(in_files)

    time_range = f"{future_slice.start}-01-01", f"{future_slice.stop}-12-31"
    base_range = (
        (f"{historical_slice.start}-01-01", f"{historical_slice.stop}-12-31")
        if historical_slice
        else None
    )

    datasets = [
        icclim.index(
            index_name=index_name,
            in_files=in_files,
            out_file=f"{tmpdir}/{index_name}.nc",
            slice_mode="year" if timeseries == "annual" else timeseries,
            time_range=time_range,
            base_period_time_range=base_range if index_name == "TX90p" else None,
        )
        for index_name in index_names
    ]

    return xr.merge(datasets).drop_dims("bounds")


def compute_trends(ds):
    datasets = []
    (lat,) = set(ds.dims) & set(ds.cf.axes["Y"])
    (lon,) = set(ds.dims) & set(ds.cf.axes["X"])
    coords_name = {
        "time": "time",
        "y": lat,
        "x": lon,
    }
    for index, da in ds.data_vars.items():
        ds = Mann_Kendall_test(
            da - da.mean("time"),
            alpha=0.05,
            method="theilslopes",
            coords_name=coords_name,
        ).compute()
        ds = ds.rename({k: v for k, v in coords_name.items() if k in ds.dims})
        ds = ds.assign_coords({dim: da[dim] for dim in ds.dims})
        datasets.append(ds.expand_dims(index=[index]))
    ds = xr.concat(datasets, "index")
    return ds


def add_bounds(ds):
    for coord in {"latitude", "longitude"} - set(ds.cf.bounds):
        ds = ds.cf.add_bounds(coord)
    return ds


def get_grid_out(request_grid_out, method):
    ds_regrid = download.download_and_transform(*request_grid_out)
    coords = ["latitude", "longitude"]
    if method == "conservative":
        ds_regrid = add_bounds(ds_regrid)
        for coord in list(coords):
            coords.extend(ds_regrid.cf.bounds[coord])
    grid_out = ds_regrid[coords]
    coords_to_drop = set(grid_out.coords) - set(coords) - set(grid_out.dims)
    grid_out = ds_regrid[coords].reset_coords(coords_to_drop, drop=True)
    grid_out.attrs = {}
    return grid_out


def compute_indices_and_trends_future(
    ds,
    index_names,
    timeseries,
    resample,
    future_slice,
    historical_slice=None,
    resample_reduction=None,
    request_grid_out=None,
    **regrid_kwargs,
):
    assert (request_grid_out and regrid_kwargs) or not (
        request_grid_out or regrid_kwargs
    )

    ds = ds.drop_vars([var for var, da in ds.data_vars.items() if len(da.dims) != 3])
    ds = ds[list(ds.data_vars)]

    # Original bounds for conservative interpolation
    if regrid_kwargs.get("method") == "conservative":
        ds = add_bounds(ds)
        bounds = [
            ds.cf.get_bounds(coord).reset_coords(drop=True)
            for coord in ("latitude", "longitude")
        ]
    else:
        bounds = []

    ds_future = select_timeseries(ds, timeseries, future_slice,index_names)
    if historical_slice:
        ds_historical = select_timeseries(ds, timeseries, historical_slice,index_names)
        ds = xr.concat([ds_historical, ds_future], "time")
    else:
        ds = ds_future

    if resample_reduction:
        resampled = ds.resample(time="1D")
        ds = getattr(resampled, resample_reduction)(keep_attrs=True)
        if resample_reduction == "sum":
            for da in ds.data_vars.values():
                da.attrs["units"] = f"{da.attrs['units']} / day"
    with tempfile.TemporaryDirectory() as tmpdir:
        ds_indices = compute_indices(
            ds,
            index_names,
            timeseries,
            tmpdir,
            future_slice=future_slice,
            historical_slice=historical_slice,
        ).compute()
        ds_trends = compute_trends(ds_indices)
        ds = ds_indices.mean("time", keep_attrs=True)
        ds = ds.merge(ds_trends)
        if request_grid_out:
            ds = diagnostics.regrid(
                ds.merge({da.name: da for da in bounds}),
                grid_out=get_grid_out(request_grid_out, regrid_kwargs["method"]),
                **regrid_kwargs,
            )
        return ds

2. Downloading and processing#

2.1. Download and transform the regridding model#

In this section, the download.download_and_transform function from the ‘c3s_eqc_automatic_quality_control’ package is employed to download daily data from the selected CORDEX regridding model, compute the precipitation-based indices for the selected temporal aggregation, calculate the mean and trend over the future projections period (2015-2099), and cache the result (to avoid redundant downloads and processing).

The regridding model is intended here as the model whose grid will be used to interpolate the others. This ensures all models share a common grid, facilitating the calculation of median values for each cell point. The regridding model within this notebook is “clmcom_eth_cosmo_crclim” but a different one can be selected by just modifying the model_regrid parameter at 1.3. Define models. It is key to highlight the importance of the chosen target grid depending on the specific application.

2.2. Download and transform models#

In this section, the download.download_and_transform function from the ‘c3s_eqc_automatic_quality_control’ package is employed to download daily data from the CORDDEX models, compute the precipitation-based indices for the selected temporal aggregation, calculate the mean and trend over the future period (2015-2099), interpolate to the regridding model’s grid (only for the cases in which it is specified, in the other cases, the original model’s grid is mantained), and cache the result (to avoid redundant downloads and processing).

model='clmcom_clm_cclm4_8_17'
model='clmcom_eth_cosmo_crclim'
model='cnrm_aladin63'
model='dmi_hirham5'
model='knmi_racmo22e'
model='mohc_hadrem3_ga7_05'
model='mpi_csc_remo2009'
model='smhi_rca4'
model='uhoh_wrf361h'

2.3. Apply land-sea mask, change attributes and cut the region to show#

This section performs the following tasks:

Cut the region of interest.
Downloads the sea mask for ERA5.
Regrids ERA5’s mask to the model_regrid grid and applies it to the regridded data
Regrids the ERA5 land-sea mask to the model’s original grid and applies it to them.
Change some variable attributes for plotting purposes.

Note: ds_interpolated contains data from the models regridded to the regridding model’s grid. model_datasets contain the same data but in the original grid of each model.

3. Plot and describe results#

This section will display the following results:

Maps representing the spatial distribution of the future trends (2015-2099) of the indices (‘CWD’, ‘R20mm’, ‘RR1’, ‘RX1day’ and ‘RX5day’) for each model individually, the ensemble median (understood as the median of the trend values of the chosen subset of models calculated for each grid cell), and the ensemble spread (derived as the standard deviation of the distribution of the chosen subset of models).
Boxplots which represent statistical distributions (PDF) built on the spatially-averaged future trend from each considered model.

3.1. Define plotting functions#

The functions presented here are used to plot the trends calculated over the future period (2015-2099) for each of the indices (‘CWD’, ‘R20mm’, ‘RR1’, ‘RX1day’ and ‘RX5day’).

For a selected index, two layout types will be displayed, depending on the chosen function:

Layout including the ensemble median and the ensemble spread for the trend: plot_ensemble() is used.
Layout including every model trend: plot_models() is employed.

trend==True allows displaying trend values over the future period, while trend==False show mean values. In this notebook, which focuses on the future period, only trend values will be shown, and, consequently, trend==True. When the trend argument is set to True, regions with no significance are hatched. For individual models, a grid point is considered to have a statistically significant trend when the p-value is lower than 0.05 (in such cases, no hatching is shown). However, for determining trend significance for the ensemble median (understood as the median of the trend values of the chosen subset of models calculated for each grid cell), reliance is placed on agreement categories, following the advanced approach proposed in AR6 IPCC on pages 1945-1950. The hatch_p_value_ensemble() function is used to distinguish, for each grid point, between three possible cases:

If more than 66% of the models are statistically significant (p-value < 0.05) and more than 80% of the models share the same sign, we consider the ensemble median trend to be statistically significant, and there is agreement on the sign. To represent this, no hatching is used.
If less than 66% of the models are statistically significant, regardless of agreement on the sign of the trend, hatching is applied (indicating that the ensemble median trend is not statistically significant).
If more than 66% of the models are statistically significant but less than 80% of the models share the same sign, we consider the ensemble median trend to be statistically significant, but there is no agreement on the sign of the trend. This is represented using crosses.

Show code cell source

Hide code cell source

#Define function to plot the caption of the figures (for the ensmble case)
def add_caption_ensemble(trend,exp):
    ref_period_str=(
    f"For this index, the reference daily 90th percentile threshold "
    f"is calculated based on the historical period (1971-2000). "
    )
    #Add caption to the figure
    match trend:
        case True:
            caption_text = (
                f"Fig {fig_number}. {long_name[index]} ('{index}') for "
                f"the temporal aggregation of '{timeseries}'. Trend for "
                f"the {exp} period ({future_slice.start}-{future_slice.stop}). "
                f"{ref_period_str if index == 'TX90p' else ''}"
                f"The layout includes data corresponding to: (a) the ensemble median "
                f"(understood as the median of the trend values of the chosen subset of models " 
                f"calculated for each grid cell) and (b) the ensemble spread "
                f"(derived as the standard deviation of the distribution of the chosen " 
                f"subset of models)."
            )
        case False:
            caption_text = (
                f"Fig {fig_number}. {long_name[index]} ('{index}') for "
                f"the temporal aggregation of '{timeseries}'. Trend for "
                f"the {exp} period ({future_slice.start}-{future_slice.stop}). "
                f"{ref_period_str if index == 'TX90p' else ''}"
                f"The layout includes data corresponding to: (a) the ensemble median "
                f"(understood as the median of the mean values of the chosen subset of models " 
                f"calculated for each grid cell) and (b) the ensemble spread "
                f"(derived as the standard deviation of the distribution of the chosen " 
                f"subset of models)."
            )
          
            
    wrapped_lines = textwrap.wrap(caption_text, width=105)
    # Add each line to the figure
    for i, line in enumerate(wrapped_lines):
        fig.text(0, -0.05  - i * 0.03, line, ha='left', fontsize=10)
    #end captioning


#Define function to plot the caption of the figures (for the individual models case)
def add_caption_models(trend,exp):
    ref_period_str=(
    f"For this index, the reference daily 90th percentile threshold "
    f"is calculated based on the historical period (1971-2000). "
    )
    #Add caption to the figure
    match trend:
        case True:
            caption_text = (
                f"Fig {fig_number}. {long_name[index]} ('{index}') for "
                f"the temporal aggregation of '{timeseries}'. Trend for the {exp} "
                f"period ({future_slice.start}-{future_slice.stop}) of each individual "
                f"{collection_id} model. " 
                f"{ref_period_str if index == 'TX90p' else ''}"
            )
        case False:
            caption_text = (
                f"Fig {fig_number}. {long_name[index]} ('{index}') for "
                f"the temporal aggregation of '{timeseries}'. Trend for the {exp} "
                f"period ({future_slice.start}-{future_slice.stop}) of each individual "
                f"{collection_id} model. " 
                f"{ref_period_str if index == 'TX90p' else ''}"
            )
    wrapped_lines = textwrap.wrap(caption_text, width=120)
    # Add each line to the figure
    for i, line in enumerate(wrapped_lines):
        fig.text(0, -0.05  - i * 0.03, line, ha='left', fontsize=10)



def hatch_p_value(da, ax, **kwargs):
    default_kwargs = {
        "plot_func": "contourf",
        "show_stats": False,
        "cmap": "none",
        "add_colorbar": False,
        "levels": [0, 0.05, 1],
        "hatches": ["", "/" * 3],
    }
    kwargs = default_kwargs | kwargs

    title = ax.get_title()
    plot_obj = plot.projected_map(da, ax=ax, **kwargs)
    ax.set_title(title)
    return plot_obj


def hatch_p_value_ensemble(trend, p_value, ax):
    n_models = trend.sizes["model"]
    robust_ratio = (p_value <= 0.05).sum("model") / n_models
    robust_ratio = robust_ratio.where(p_value.notnull().any("model"))
    signs = xr.concat([(trend > 0).sum("model"), (trend < 0).sum("model")], "sign")
    sign_ratio = signs.max("sign") / n_models
    robust_threshold = 0.66
    sign_ratio = sign_ratio.where(robust_ratio > robust_threshold)
    for da, threshold, character in zip(
        [robust_ratio, sign_ratio], [robust_threshold, 0.8], ["/", "\\"]
    ):
        hatch_p_value(da, ax=ax, levels=[0, threshold, 1], hatches=[character * 3, ""])


def set_extent(da, axs, area):
    extent = [area[i] for i in (1, 3, 2, 0)]
    for i, coord in enumerate(extent):
        extent[i] += -1 if i % 2 else +1
    for ax in axs:
        ax.set_extent(extent)


def plot_models(
    data,
    da_for_kwargs=None,
    p_values=None,
    col_wrap=4 if collection_id=="CMIP6" else 3,
    subplot_kw={"projection": ccrs.PlateCarree()},
    figsize=None,
    layout="constrained",
    area=area,
    **kwargs,
):
    if isinstance(data, dict):
        assert da_for_kwargs is not None
        model_dataarrays = data
    else:
        da_for_kwargs = da_for_kwargs or data
        model_dataarrays = dict(data.groupby("model"))

    if p_values is not None:
        model_p_dataarrays = (
            p_values if isinstance(p_values, dict) else dict(p_values.groupby("model"))
        )
    else:
        model_p_dataarrays = None

    # Get kwargs
    default_kwargs = {"robust": True, "extend": "both"}
    kwargs = default_kwargs | kwargs
    kwargs = xr.plot.utils._determine_cmap_params(da_for_kwargs.values, **kwargs)

    fig, axs = plt.subplots(
        *(col_wrap, math.ceil(len(model_dataarrays) / col_wrap)),
        subplot_kw=subplot_kw,
        figsize=figsize,
        layout=layout,
    )
    axs = axs.flatten()
    for (model, da), ax in zip(model_dataarrays.items(), axs):
        pcm = plot.projected_map(
            da, ax=ax, show_stats=False, add_colorbar=False, **kwargs
        )
        ax.set_title(model)
        if model_p_dataarrays is not None:
            hatch_p_value(model_p_dataarrays[model], ax)
    set_extent(da_for_kwargs, axs, area)
    fig.colorbar(
        pcm,
        ax=axs.flatten(),
        extend=kwargs["extend"],
        location="right",
        label=f"{da_for_kwargs.attrs.get('long_name', '')} [{da_for_kwargs.attrs.get('units', '')}]",
    )
    return fig


def plot_ensemble(
    da_models,
    da_era5=None,
    p_value_era5=None,
    p_value_models=None,
    subplot_kw={"projection": ccrs.PlateCarree()},
    figsize=None,
    layout="constrained",
    cbar_kwargs=None,
    area=area,
    cmap_bias=None,
    cmap_std=None,
    **kwargs,
):
    # Get kwargs
    default_kwargs = {"robust": True, "extend": "both"}
    kwargs = default_kwargs | kwargs
    kwargs = xr.plot.utils._determine_cmap_params(
        da_models.values if da_era5 is None else da_era5.values, **kwargs
    )
    if da_era5 is None and cbar_kwargs is None:
        cbar_kwargs = {"orientation": "horizontal"}

    # Figure
    fig, axs = plt.subplots(
        *(1 if da_era5 is None else 2, 2),
        subplot_kw=subplot_kw,
        figsize=figsize,
        layout=layout,
    )
    axs = axs.flatten()
    axs_iter = iter(axs)

    # ERA5
    if da_era5 is not None:
        ax = next(axs_iter)
        plot.projected_map(
            da_era5, ax=ax, show_stats=False, cbar_kwargs=cbar_kwargs, **kwargs
        )
        if p_value_era5 is not None:
            hatch_p_value(p_value_era5, ax=ax)
        ax.set_title("(a) ERA5")

    # Median
    ax = next(axs_iter)
    median = da_models.median("model", keep_attrs=True)
    plot.projected_map(
        median, ax=ax, show_stats=False, cbar_kwargs=cbar_kwargs, **kwargs
    )
    if p_value_models is not None:
        hatch_p_value_ensemble(trend=da_models, p_value=p_value_models, ax=ax)
    ax.set_title("(b) Ensemble Median" if da_era5 is not None else "(a) Ensemble Median")

    # Bias
    if da_era5 is not None:
        ax = next(axs_iter)
        with xr.set_options(keep_attrs=True):
            bias = median - da_era5
        plot.projected_map(
            bias,
            ax=ax,
            show_stats=False,
            center=0,
            cbar_kwargs=cbar_kwargs,
            **(default_kwargs | {"cmap": cmap_bias}),
        )
        ax.set_title("(c) Ensemble Median Bias")

    # Std
    ax = next(axs_iter)
    std = da_models.std("model", keep_attrs=True)
    plot.projected_map(
        std,
        ax=ax,
        show_stats=False,
        cbar_kwargs=cbar_kwargs,
        **(default_kwargs | {"cmap": cmap_std}),
    )
    ax.set_title("(d) Ensemble Standard Deviation" if da_era5 is not None else "(b) Ensemble Standard Deviation")

    set_extent(da_models, axs, area)
    return fig

3.2. Plot ensemble maps#

In this section, we invoke the plot_ensemble() function to visualise the trend calculated over the future period (2015-2099) for the model ensemble across Europe. Note that the model data used in this section has previously been interpolated to the “regridding model” grid ("clmcom_eth_cosmo_crclim" for this notebook).

Specifically, for each of the indices (‘CWD’, ‘R20mm’, ‘RR1’, ‘RX1day’ and ‘RX5day’), this section presents a single layout including trend values of the future period (2015-2099) for: (a) the ensemble median (understood as the median of the trend values of the chosen subset of models calculated for each grid cell) and (b) the ensemble spread (derived as the standard deviation of the distribution of the chosen subset of models).

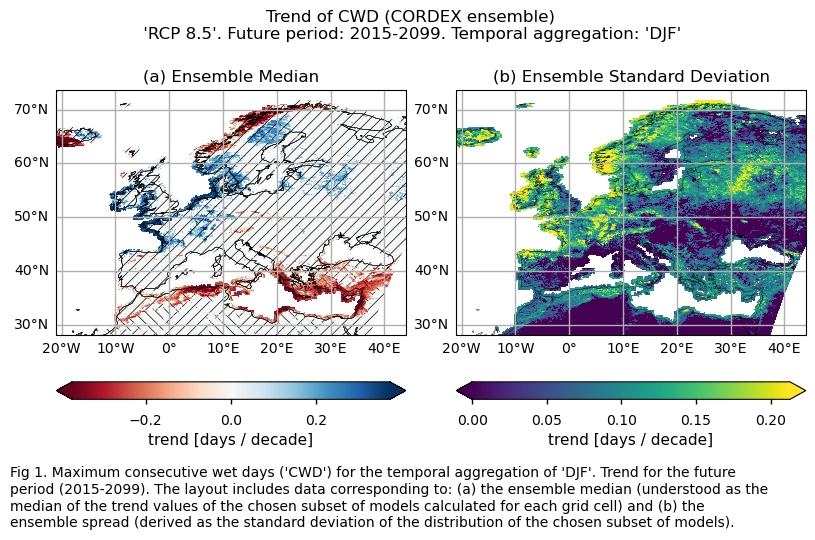
../../_images/da1342e972c3319301e79bfbe5f2440f65b01d8a4c8101a195243f02d1b8ae48.png

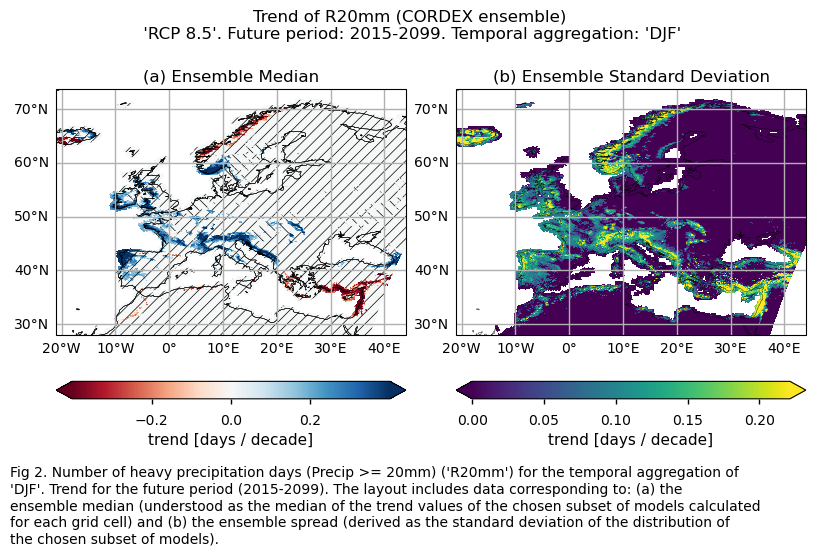
../../_images/e39e6e011ba6df39f694e99d52116567847532261de5752312e4faeba6c6c326.png

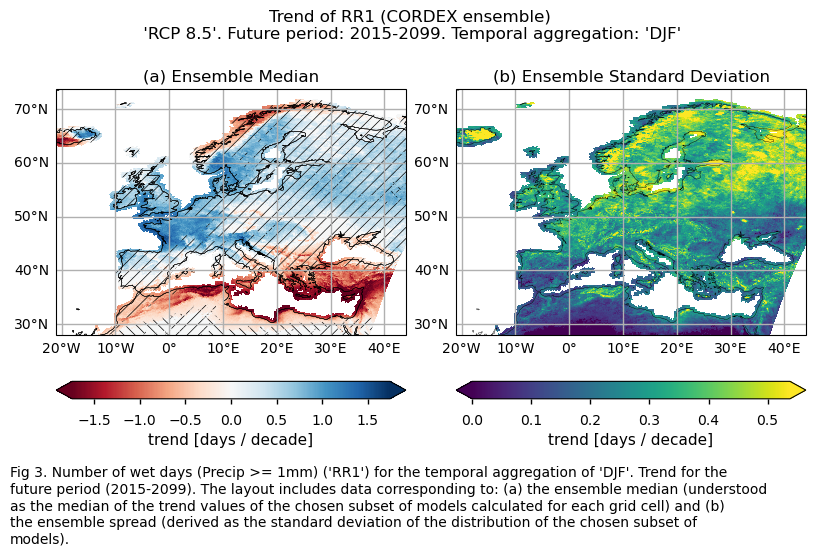
../../_images/062b3a43a3f47dfe35337796c0c15e573ffcf08c7c386ee71ba5f6325a46caf8.png

../../_images/69ca1bc9a605e8fa955b3556f2664cbdd585b98d4be1e297890b6aee85a8abeb.png

../../_images/38bbeaee38d3f3239104156e0eb6978cd492be30483de47885dbb93ad3e5859e.png

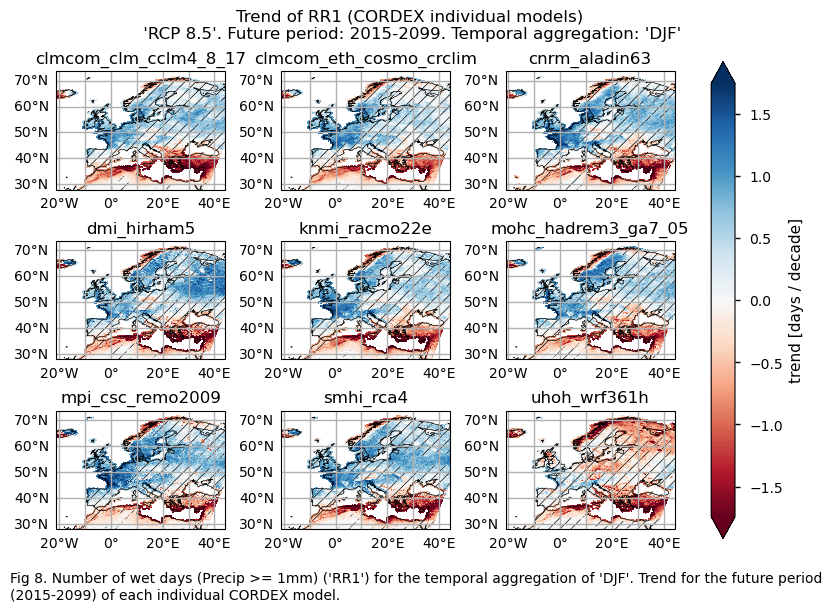
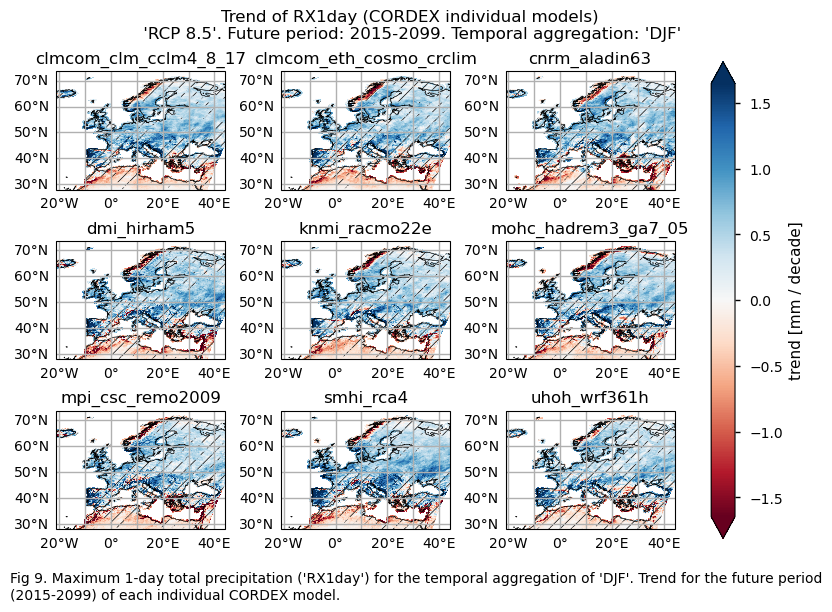
3.3. Plot model maps#

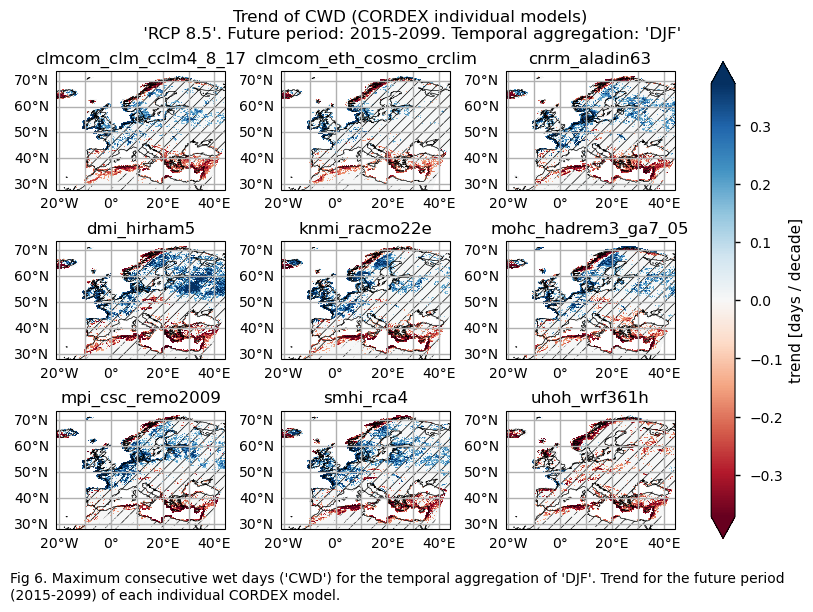
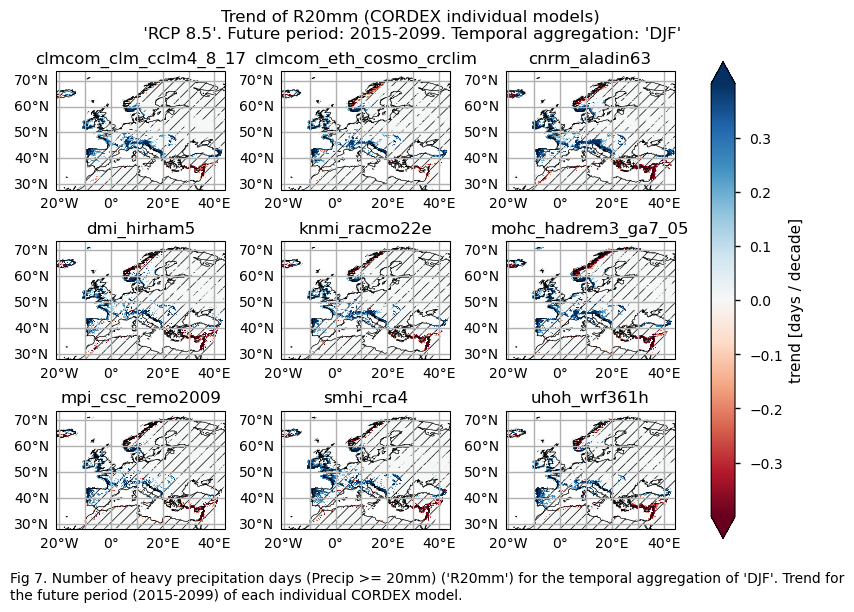
In this section, we invoke the plot_models() function to visualise the trend calculated over the future period (2015-2099) for every model individually across Europe. Note that the model data used in this section maintains its original grid.

Specifically, for each of the indices (‘CWD’, ‘R20mm’, ‘RR1’, ‘RX1day’ and ‘RX5day’), this section presents a single layout including the trend for the future period (2015-2099) of every model.

../../_images/635115e77968d9357443fba733d933f9446dd8453f401828d7a3998d9cb870a7.png

../../_images/f1d4559617a447792898c42b205831c95ec66a5852ca6bbd8abb8a21c249ab87.png

../../_images/aed2cfad919d6694bb2630b848d55bd1530b077eec5b68e771db7971624a53cb.png

../../_images/e7f2e265dd8d62e4e0aa12253db9a401fa5df1dc44519e47cba41df75893adc5.png

../../_images/15e2c1be057bd1d857d83b6c334022fcd590101d97961d38d37b92466969867e.png

3.4. Boxplots of the future trend#

Finally, we present boxplots representing the ensemble distribution of each climate model trend calculated over the future period (2015-2099) across Europe.

Dots represent the spatially-averaged future trend over the selected region (change of the number of days per decade) for each model (grey) and the ensemble mean (blue). The ensemble median is shown as a green line. Note that the spatially averaged values are calculated for each model from its original grid (i.e., no interpolated data has been used here).

The boxplot visually illustrates the distribution of trends (or bias trends) among the climate models, with the box covering the first quartile (Q1 = 25th percentile) to the third quartile (Q3 = 75th percentile), and a green line indicating the ensemble median (Q2 = 50th percentile). Whiskers extend from the edges of the box to show the full data range.

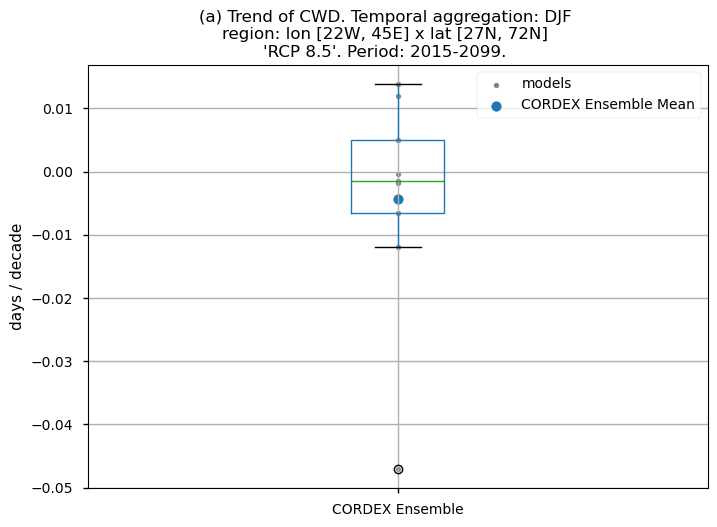
../../_images/7e0d6af79035cca9ee722f0bd38391057998ba06cbff1b62fce697966a949556.png

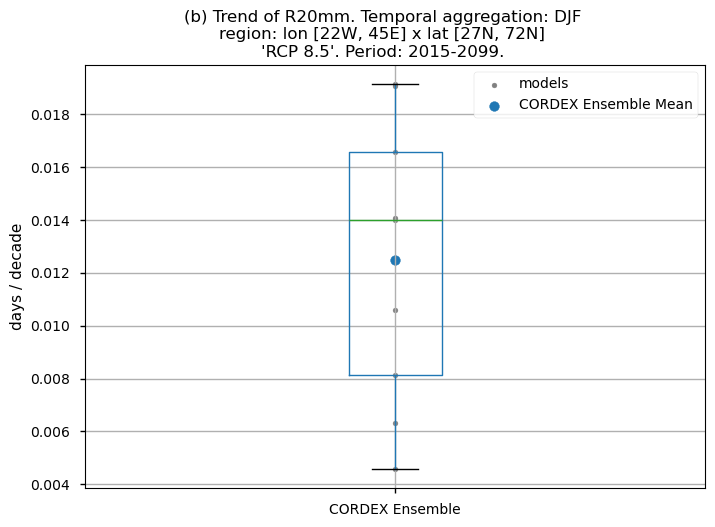
../../_images/7e77fa61a54e1ca2c72b42cd8e1b7c5880428aa12c1c63421b268c5abe2a417c.png

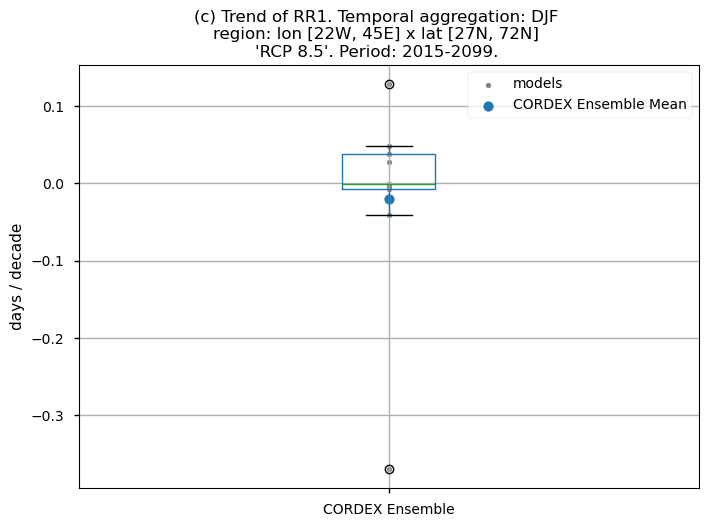
../../_images/a46099aef35c7f2727a1843e9f2ea42a838f1d391572fed04ba1f70fc328d425.png

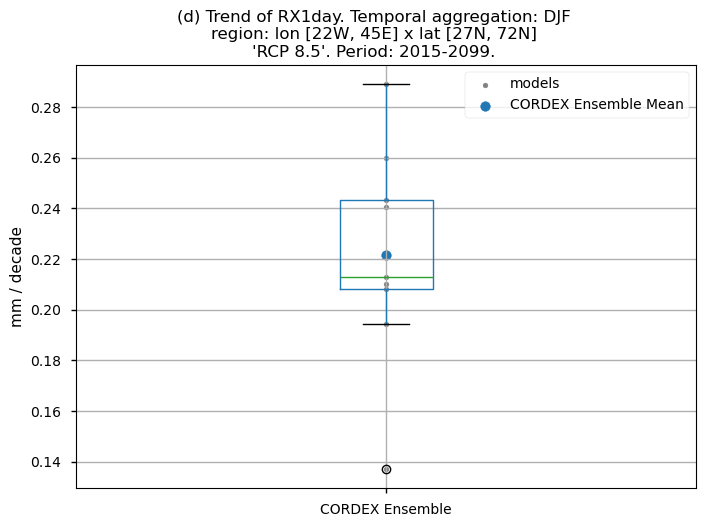
../../_images/07f5ae89e3ed0a27e4c02043df148195a6f826269b3e6857c0b0103a1899e899.png

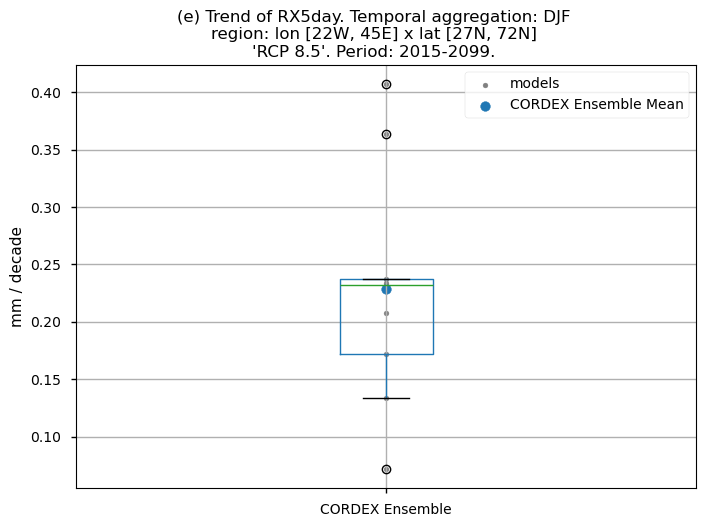
../../_images/3695f151501f796442dad6e035d9248135e5abb79d47bfc609460e54929af47f.png

Fig 11. Boxplots illustrating the future trends (2015-2099) of the ensemble distribution for the precipitation-based indices: (a) 'CWD', (b) R20mm, (c) RR1, (d) RX1day and (e) RX5day. The distribution is created by considering spatially averaged trends across Europe. The ensemble mean and the ensemble median trends are both included. Outliers in the distribution are denoted by a grey circle with a black contour.

3.5. Results summary and discussion#

The level of agreement among models for precipitation-based indices projections is lower than for maximum temperature indices. Additionally, the trends are clearly less robust compared to maximum temperature. This is evident when comparing the findings of this assessment with those presented in “CORDEX Climate Projections: Evaluating Uncertainty in Projected Changes in Extreme Temperature Indices for the Reinsurance Sector.”
The future trend (calculated over the 2015-2099 period) in precipitation-based indices for the temporal aggregation of DJF largely depends on the considered index.
The maximum Consecutive Wet Days (CWD) are projected to increase on the Atlantic coasts of the western part of the continent (except in the central and northwest of Scandinavia and the west of Iceland, where it is expected to decrease). Decreases are also expected on the southernmost and eastern coasts of the Mediterranean basin. No significant trend is detected in the rest of the regions.
The number of heavy precipitation days (R20mm) is expected to increase in the west of the Iberian Peninsula, southwest of France, west of the United Kingdom, south of Norway, Balkan coasts, and some parts of the northern part of Italy and southeast of France. Decreases are expected in the Mediterranean coastal areas of Turkey. No significant trend is present in the model output for the rest of the regions.
Increases in the number of wet days (RR1) are projected to increase in the Scandinavian Peninsula (in contrast to the decrease expected in the western coastal regions), United Kingdom, center, center-east, and northeast of Europe. Conversely, decreases are expected in the Mediterranean regions of Africa and the eastern part of the Mediterranean basin.
The future trend of the maximum 1-day total precipitation (RX1day) and maximum 5-day total precipitation (RX5day) have a similar spatial pattern. An increase is projected for most of Europe (indicating more extreme precipitation events), with the exception of the Mediterranean regions of Africa and the southeastern part of the Mediterranean basin, and the center-west and northwestern Atlantic coastal regions of Scandinavia where a decrease is expected.
The boxplots displaying spatially-averaged values of the future trend for the temporal aggregation of winter (DJF) reveal diverse outcomes depending on the index under consideration. Notably, significant inter-model variability is evident for certain indices, whose interquartile range encompasses trends of varying directions. These are the cases of CWD and RR1. The other indices show a positive trend with outliers in some cases (RX5day).
It is important to emphasise that the boxplots present spatially-averaged values, and their interpretation should be approached with caution, as the outcomes can vary significantly when considering different regions across Europe. For regional analyses, it is essential to focus solely on the region of interest, as the influence of other European regions may distort the results, leading to conclusions that do not accurately reflect the specific area under study.
What do the results mean for users? Are the biases relevant?
- The results of this notebook are strongly influenced by the index and region. Projected changes for RR1, RX1day, and RX5day display similar spatial patterns across the subset of models considered. In contrast, CWD and R20mm show more scattered spatial patterns, with regions that have significant trend signals exhibiting high uncertainty (inter-model spread).
- Findings from another assessment of the same indices and seasonal aggregation (DJF) for the historical period 1971-2000, which evaluated biases (“CORDEX Climate Projections: evaluating bias in precipitation-based indices for impact models”), should also be taken into account. The high uncertainties in both assessments suggest that users should bias-correct precipitation-based indices before using them for specific applications [5].

RESULTS NOTE:
It is important to note that the results presented are specific to the 9 models chosen, and users should aim to assess as wide a range of models as possible before making a sub-selection.

ℹ️ If you want to know more#

Key resources#

Some key resources and further reading were linked throughout this assessment.

The CDS catalogue entries for the data used were:

CORDEX regional climate model data on single levels (Daily mean - Mean precipitation flux): https://cds.climate.copernicus.eu/datasets/projections-cordex-domains-single-levels?tab=overview

Code libraries used:

C3S EQC custom functions, c3s_eqc_automatic_quality_control, prepared by B-Open
icclim Python package

References#

[1] Panagos, P., Borrelli, P., Poesen, J., Ballabio, C., Lugato, E., Meusburger, K., Montanarella, L., Alewell, C. (2015). The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy, 54, pp. 438-447. https://doi.org/10.1016/j.envsci.2015.08.012

[2] Salvati, L., Carlucci, M. (2013). The impact of mediterranean land degradation on agricultural income: a short-term scenario. Land Use Policy, 32, pp. 302-308. https://doi.org/10.1016/j.landusepol.2012.11.007

[3] Rummukainen, M. (2010). State-of-the-art with regional climate models. WIREs Clim Change, 1: 82-96. https://doi.org/10.1002/wcc.8

[4] Silje Lund Sørland et al. (2018). Bias patterns and climate change signals in GCM-RCM model chains. Environ. Res. Lett. 13 074017. https://doi.org/10.1088/1748-9326/aacc77

[5] Teutschbein, C., Seibert, J. (2012). Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. Journal of Hydrology, Volumes 456–457, pp. 12-29. https://doi.org/10.1016/j.jhydrol.2012.05.052

Projected changes in precipitation-based indices for impact models

Contents

5.2.4. Projected changes in precipitation-based indices for impact models#

🌍 Use case: Verification of precipitation indices used as proxies for rainfall erosivity in Europe under future climate scenarios.#

❓ Quality assessment question#

📢 Quality assessment statement#

📋 Methodology#

📈 Analysis and results#

1. Parameters, requests and functions definition#

1.1. Import packages#

1.2. Define Parameters#

1.3. Define models#

1.4. Define land-sea mask request#

1.5. Define model requests#

1.6. Functions to cache#

2. Downloading and processing#

2.1. Download and transform the regridding model#

2.2. Download and transform models#

2.3. Apply land-sea mask, change attributes and cut the region to show#

3. Plot and describe results#

3.1. Define plotting functions#

3.2. Plot ensemble maps#

3.3. Plot model maps#

3.4. Boxplots of the future trend#

3.5. Results summary and discussion#

ℹ️ If you want to know more#

Key resources#

References#