
5.1.4. Biases in energy-consumption-related indices in Europe#
Production date: 22-05-2024
Produced by: CMCC foundation - Euro-Mediterranean Center on Climate Change. Albert Martinez Boti.
🌍 Use case: Assessing possible impacts of climate change on energy demand in Europe#
❓ Quality assessment question#
How well do the CMIP6 projections represent Energy Degree Days climatology and trend over a historic period?
Sectors affected by climate change are varied including agriculture [1], forest ecosystems [2], and energy consumption [3]. Under projected future global warming over Europe [4][5], the current increase in energy demand is expected to persist until the end of this century and beyond [6]. Identifying which climate-change-related impacts are likely to increase, by how much, and inherent regional patterns, is important for any effective strategy for managing future climate risks. This notebook utilises data from a subset of models from CMIP6 Global Climate Models (GCMs) and compares them with ERA5 reanalysis, serving as the reference product. Two energy-consumption-related indices are calculated from daily mean temperatures using the icclim Python package: Cooling Degree Days (CDDs) and Heating Degree Days (HDDs). Degree days measure how much warmer or colder it is compared to standard temperatures (usually 15.5°C for heating and 22°C for cooling). Higher degree day numbers indicate more extreme temperatures, which typically lead to increased energy use for heating or cooling buildings. In the presented code, CDD calculations use summer aggregation (CDD22), while HDD calculations focus on winter (HDD15.5), presenting results as daily averages rather than cumulative values. Within this notebook, these calculations are performed over the historical period spanning from 1971 to 2000. It is important to note that the results presented here pertain to a specific subset of the CMIP6 ensemble and may not be generalisable to the entire dataset. Also note that a separate assessment examines the representation of trends of these indices for the same models during a fixed future period (2015-2099), while another assessment looks at the projected climate signal of these indices for the same models at a 2°C Global Warming Level.
📢 Quality assessment statement#
These are the key outcomes of this assessment
CMIP6 projections provide valuable insights into trends and climatology of Energy Degree Days across Europe, though with inherent uncertainties, and differences compared to the reference dataset (ERA5). During the historical period (1971-2000), GCMs exhibited biases in capturing both mean values and trends for energy-consumption-related indices.
For the 16 models considered, biases were observed in mean values of Heating Degree Days (‘HDD15.5’) over DJF and Cooling Degree Days (‘CDD22’) over JJA. Specifically, for most of the models, there is an overestimation of HDD15.5 mean values for DJF (except in regions with complex orography where there was underestimation) and CDD22 mean values for JJA across most of the Mediterranean Basin.
The subset of CMIP6 models show a decrease in the energy needed for heating during winter within the historical period across Europe, especially in the eastern and northern regions. This aligns with results obtained using the ERA5 reference product, except in the Balkans where there is an increase in required heating energy during this period. The ERA5 reference product also shows an increase of the amount of energy needed for cooling buildings in summer during this period, particularly across the Mediterranean Basin. This trend is well captured by the subset of CMIP6 models. Depending on the region, these results may enhance confidence in using these models for analysing future trends, although they do not guarantee accuracy.
Despite the biases and high inter-model spread in some regions, the outcomes of this notebook offer valuable insights for decisions sensitive to future energy demand. These results may enhance confidence in using these models to analyse future trends, although their accuracy is not assured. To improve the accuracy of these insights, biases should be considered and corrected [6][7].
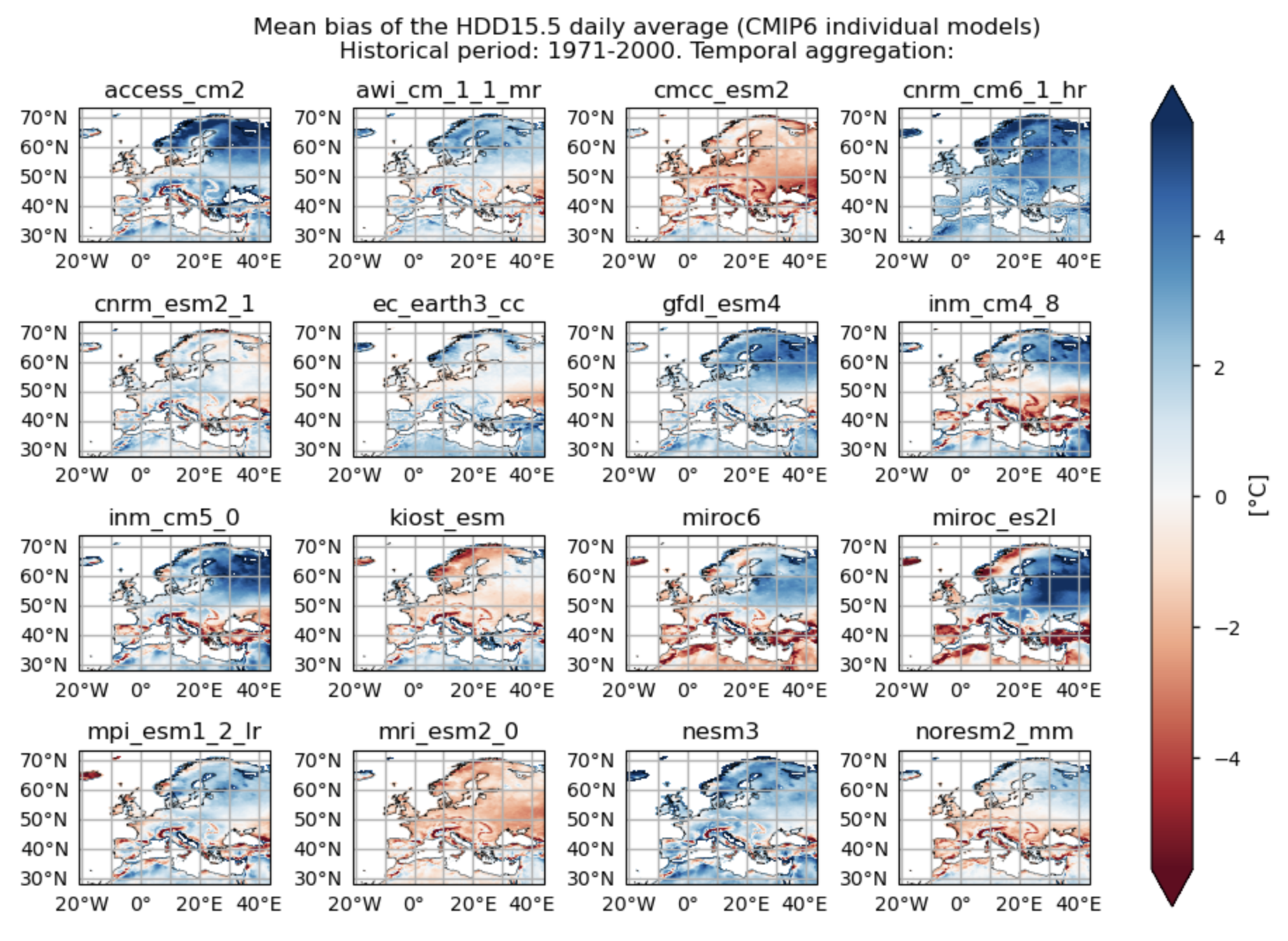
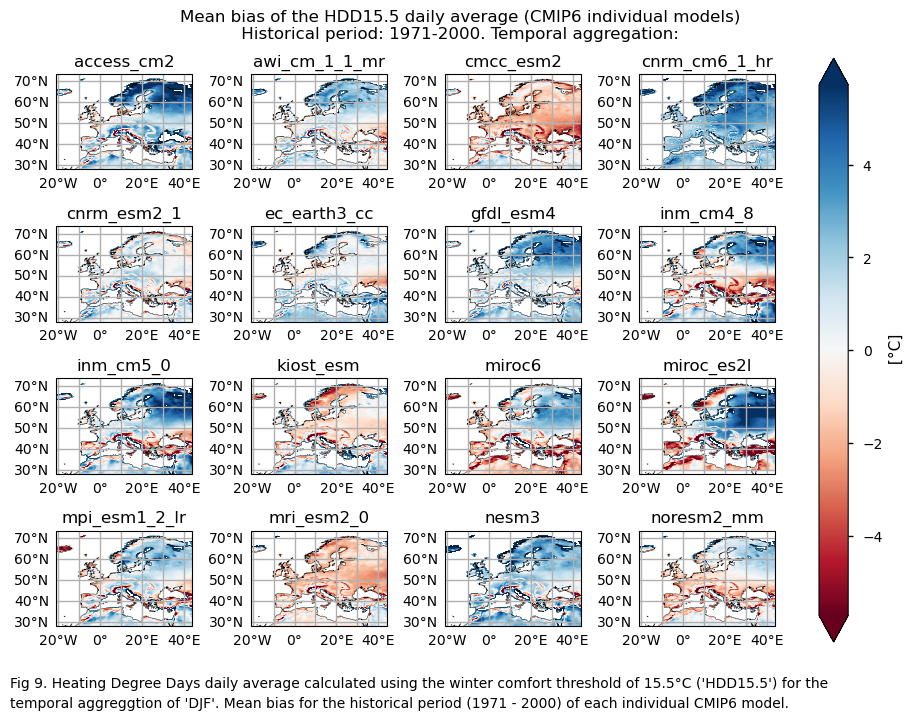
Fig. 5.1.4.1 Heating Degree Days daily average calculated using the winter comfort threshold of 15.5°C (‘HDD15.5’) for the temporal aggreggtion of ‘DJF’. Mean bias for the historical period (1971 - 2000) of each individual CMIP6 model. The colorbar chosen for representing biases for the HDD15.5 index ranges from red to blue. In this color scheme, negative bias values (red colors) indicate that the Heating Degree Days displayed by the models are lower than those shown by ERA5. Instead, blueish colors denote more Heating Degree Days, indicating a positive bias compared to ERA5. This selection is based on the rationale that more Heating Degree Days are associated with colder conditions, typically represented by blueish colors, while fewer Heating Degree Days imply warmer conditions, depicted by reddish colors.#
📋 Methodology#
The reference methodology used here for the indices calculation is similar to the one followed by Scoccimarro et al., (2023) [8]. However the thermal comfort thresholds used in this notebook are slightly different. A winter comfort temperature of 15.5°C and a summer comfort temperature of 22.0°C are used here (as in the CDS application). In the presented code, the CDD calculations are based on the JJA aggregation, with a comfort temperature of 22°C (CDD22), while HDD calculations focus on winter (DJF) with a comfort temperature of 15.5°C (HDD15.5). More specifically, to calculate CDD22, the sum of the differences between the daily mean temperature and the thermal comfort temperature of 22°C is computed. This calculation occurs only when the mean temperature is above the thermal comfort level; otherwise, the CDD22 for that day is set to 0. For example, a day with a mean temperature of 28°C would result in 6°C. Two consecutive hot days like this would total 12°C over the two-day period. Similarly, to calculate HDD15.5, the sum of the differences between the thermal comfort temperature of 15.5°C and the daily mean temperature is determined. This happens only when the mean temperature is below the thermal comfort level; otherwise, the HDD15.5 for that day is set to 0. Finally, to obtain more intuitive values, the sum is averaged over the number of days in the season to produce daily average values. This approach differs from the CDS application, where both the sum over a period and the daily average values can be displayed. In Spinoni et al., (2018) [6], as well as in the CDS application, more advanced methods for calculating CDD and HDD involve considering maximum, minimum, and mean temperatures. However, to prevent overloading the notebook and maintain simplicity while ensuring compatibility with the icclim Python package, we opted to utilise a single variable (2m mean temperature).
This notebook provides an assessment of the systematic errors (trend and climate mean) in a subset of 16 models from CMIP6. It achieves this by comparing the model predictions with the ERA5 reanalysis for the energy-consumption-related indices ‘HDD15.5’ and ‘CDD22’ for the historical period spanning from 1971 to 2000. In particular, spatial patterns of climate mean and trend, along with biases, are examined and displayed for each model and the ensemble median (calculated for each grid cell). Additionally, spatially-averaged trend values are analysed and presented using box plots to provide an overview of trend behavior across the distribution of the chosen subset of models when averaged across Europe.
The analysis and results follow the next outline:
1. Parameters, requests and functions definition
📈 Analysis and results#
1. Parameters, requests and functions definition#
1.1. Import packages#
Show code cell source
Hide code cell source
import math
import tempfile
import warnings
import textwrap
warnings.filterwarnings("ignore")
import cartopy.crs as ccrs
import icclim
import matplotlib.pyplot as plt
import xarray as xr
from c3s_eqc_automatic_quality_control import diagnostics, download, plot, utils
from xarrayMannKendall import Mann_Kendall_test
plt.style.use("seaborn-v0_8-notebook")
plt.rcParams["hatch.linewidth"] = 0.5
1.2. Define Parameters#
In the “Define Parameters” section, various customisable options for the notebook are specified:
The initial and ending year used for the historical period can be specified by changing the parameters
year_startandyear_stop(1971-2000 is chosen for consistency between CORDEX and CMIP6).index_timeseriesis a dictionary that set the temporal aggregation for every index considered within this notebook (‘HDD15.5’ and ‘CDD22’). In the presented code, the CDD calculations are always based on the JJA aggregation, with a comfort temperature of 22°C (CDD22), while HDD calculations focus on winter (DJF) with a comfort temperature of 15.5°C (HDD15.5).collection_idsets the family of models. Only CMIP6 is implemented for this notebook.areaallows specifying the geographical domain of interest.The
interpolation_methodparameter allows selecting the interpolation method when regridding is performed over the indices.The
chunkselection allows the user to define if dividing into chunks when downloading the data on their local machine. Although it does not significantly affect the analysis, it is recommended to keep the default value for optimal performance.
Show code cell source
Hide code cell source
# Time period
year_start = 1971
year_stop = 2000
# Choose annual or seasonal timeseries
index_timeseries = {
"HDD15.5": "DJF",
"CDD22": "JJA",
}
if "annual" in index_timeseries.values():
assert set(index_timeseries.values()) == {"annual"}
# Interpolation method
interpolation_method = "bilinear"
# Select the family of models
collection_id = "CMIP6"
assert collection_id in ("CMIP6")
# Area to show
area = [72, -22, 27, 45]
# Chunks for download
chunks = {"year": 1}
1.3. Define models#
The following climate analyses are performed considering a subset of GCMs from CMIP6. Models names are listed in the parameters below. Some variable-dependent parameters are also selected.
The selected CMIP6 models have available both experiments the historical and the SSP8.5.
Show code cell source
Hide code cell source
# Define models
models_cmip6 = (
"access_cm2",
"awi_cm_1_1_mr",
"cmcc_esm2",
"cnrm_cm6_1_hr",
"cnrm_esm2_1",
"ec_earth3_cc",
"gfdl_esm4",
"inm_cm4_8",
"inm_cm5_0",
"kiost_esm",
"mpi_esm1_2_lr",
"miroc6",
"miroc_es2l",
"mri_esm2_0",
"noresm2_mm",
"nesm3",
)
# Colormaps
cmaps = {"HDD15.5": "Blues", "CDD22": "Reds"}
cmaps_trend = cmaps_bias = {"HDD15.5": "RdBu", "CDD22": "RdBu_r"}
#Define dictionaries to use in titles and caption
long_name = {
"HDD15.5":"Heating Degree Days daily average calculated using the winter comfort threshold of 15.5°C" ,
"CDD22":"Cooling Degree Days daily average calculated using the summer comfort threshold of 22°C",
}
1.4. Define ERA5 request#
Within this notebook, ERA5 serves as the reference product. In this section, we set the required parameters for the cds-api data-request of ERA5.
Show code cell source
Hide code cell source
request_era = (
"reanalysis-era5-single-levels",
{
"product_type": "reanalysis",
"format": "netcdf",
"time": [f"{hour:02d}:00" for hour in range(24)],
"variable": "2m_temperature",
"year": [
str(year) for year in range(year_start - 1, year_stop + 1)
], # Include D(year-1)
"month": [f"{month:02d}" for month in range(1, 13)],
"day": [f"{day:02d}" for day in range(1, 32)],
"area": area,
},
)
request_lsm = (
request_era[0],
request_era[1]
| {
"year": "1940",
"month": "01",
"day": "01",
"time": "00:00",
"variable": "land_sea_mask",
},
)
1.5. Define model requests#
In this section we set the required parameters for the cds-api data-request.
When weights = True, spatial weighting is applied for calculations requiring spatial data aggregation. This is particularly relevant for CMIP6 GCMs with regular lon-lat grids that do not consider varying surface extensions at different latitudes.
Show code cell source
Hide code cell source
request_cmip6 = {
"format": "zip",
"temporal_resolution": "daily",
"experiment": "historical",
"variable": "near_surface_air_temperature",
"year": [
str(year) for year in range(year_start - 1, year_stop + 1)
], # Include D(year-1)
"month": [f"{month:02d}" for month in range(1, 13)],
"day": [f"{day:02d}" for day in range(1, 32)],
"area": area,
}
model_requests = {}
for model in models_cmip6:
model_requests[model] = (
"projections-cmip6",
download.split_request(request_cmip6 | {"model": model}, chunks=chunks),
)
1.6. Functions to cache#
In this section, functions that will be executed in the caching phase are defined. Caching is the process of storing copies of files in a temporary storage location, so that they can be accessed more quickly. This process also checks if the user has already downloaded a file, avoiding redundant downloads.
Functions description:
The
select_timeseriesfunction subsets the dataset based on the chosentimeseriesparameter.The
compute_indicesfunction utilises the icclim package to calculate the energy-consumption-related indices.The
compute_trendsfunction employs the Mann-Kendall test for trend calculation.Finally, the
compute_indices_and_trendscomputes the daily mean temperature (only if we are dealing with ERA5), calculates the energy consumption-related indices for the corresponding temporal aggregation using thecompute_indicesfunction, determines the indices mean over the historical period (1971-2000), obtain the trends using thecompute_trendsfunction, and offers an option for regridding to ERA5 if required.
Show code cell source
Hide code cell source
def select_timeseries(ds, index_timeseries, year_start, year_stop):
timeseries = set(index_timeseries.values())
if timeseries == {"annual"}:
return ds.sel(time=slice(str(year_start), str(year_stop)))
assert "annual" not in timeseries
return ds.sel(time=slice(f"{year_start-1}-12", f"{year_stop}-11"))
def compute_indices(ds, index_timeseries, tmpdir):
labels, datasets = zip(*ds.groupby("time.year"))
paths = [f"{tmpdir}/{label}.nc" for label in labels]
datasets = [ds.chunk(-1) for ds in datasets]
xr.save_mfdataset(datasets, paths)
ds = xr.open_mfdataset(paths)
in_files = f"{tmpdir}/rechunked.zarr"
chunks = {dim: -1 if dim == "time" else "auto" for dim in ds.dims}
ds.chunk(chunks).to_zarr(in_files)
dataarrays = []
for index_name, timeseries in index_timeseries.items():
kwargs = {
"in_files": in_files,
"out_file": f"{tmpdir}/{index_name}.nc",
"slice_mode": "year" if timeseries == "annual" else timeseries,
}
if index_name == "HDD15.5":
ds_index = icclim.index(
**kwargs,
index_name="deficit",
threshold=icclim.build_threshold("15.5 degC"),
)
elif index_name == "CDD22":
ds_index = icclim.excess(
**kwargs,
threshold=icclim.build_threshold("22 degC"),
)
else:
raise NotImplementedError(f"{index_name=}")
(da,) = ds_index.drop_dims("bounds").data_vars.values()
num_days = {"DJF": 90, "MAM": 92, "JJA": 92, "SON": 91}
with xr.set_options(keep_attrs=True):
da /= (
num_days[timeseries]
if timeseries != "annual"
else sum(num_days.values())
)
da.attrs["units"] = da.attrs["units"].replace(" d", "")
dataarrays.append(da.rename(index_name))
return xr.merge(dataarrays)
def compute_trends(ds):
datasets = []
(lat,) = set(ds.dims) & set(ds.cf.axes["Y"])
(lon,) = set(ds.dims) & set(ds.cf.axes["X"])
coords_name = {
"time": "time",
"y": lat,
"x": lon,
}
for index, da in ds.data_vars.items():
ds = Mann_Kendall_test(
da - da.mean("time"),
alpha=0.05,
method="theilslopes",
coords_name=coords_name,
).compute()
ds = ds.rename({k: v for k, v in coords_name.items() if k in ds.dims})
ds = ds.assign_coords({dim: da[dim] for dim in ds.dims})
datasets.append(ds.expand_dims(index=[index]))
ds = xr.concat(datasets, "index")
return ds
def add_bounds(ds):
for coord in {"latitude", "longitude"} - set(ds.cf.bounds):
ds = ds.cf.add_bounds(coord)
return ds
def get_grid_out(request_grid_out, method):
ds_regrid = download.download_and_transform(*request_grid_out)
coords = ["latitude", "longitude"]
if method == "conservative":
ds_regrid = add_bounds(ds_regrid)
for coord in list(coords):
coords.extend(ds_regrid.cf.bounds[coord])
grid_out = ds_regrid[coords]
coords_to_drop = set(grid_out.coords) - set(coords) - set(grid_out.dims)
grid_out = ds_regrid[coords].reset_coords(coords_to_drop, drop=True)
grid_out.attrs = {}
return grid_out
def compute_indices_and_trends(
ds,
index_timeseries,
year_start,
year_stop,
resample_reduction=None,
request_grid_out=None,
**regrid_kwargs,
):
assert (request_grid_out and regrid_kwargs) or not (
request_grid_out or regrid_kwargs
)
ds = ds.drop_vars([var for var, da in ds.data_vars.items() if len(da.dims) != 3])
ds = ds[list(ds.data_vars)]
# Original bounds for conservative interpolation
if regrid_kwargs.get("method") == "conservative":
ds = add_bounds(ds)
bounds = [
ds.cf.get_bounds(coord).reset_coords(drop=True)
for coord in ("latitude", "longitude")
]
else:
bounds = []
ds = select_timeseries(ds, index_timeseries, year_start, year_stop)
if resample_reduction:
resampled = ds.resample(time="1D")
ds = getattr(resampled, resample_reduction)(keep_attrs=True)
if resample_reduction == "sum":
for da in ds.data_vars.values():
da.attrs["units"] = f"{da.attrs['units']} / day"
with tempfile.TemporaryDirectory() as tmpdir:
ds_indices = compute_indices(ds, index_timeseries, tmpdir).compute()
ds_trends = compute_trends(ds_indices)
ds = ds_indices.mean("time", keep_attrs=True)
ds = ds.merge(ds_trends)
if request_grid_out:
ds = diagnostics.regrid(
ds.merge({da.name: da for da in bounds}),
grid_out=get_grid_out(request_grid_out, regrid_kwargs["method"]),
**regrid_kwargs,
)
return ds
2. Downloading and processing#
2.1. Download and transform ERA5#
In this section, the download.download_and_transform function from the ‘c3s_eqc_automatic_quality_control’ package is employed to download ERA5 reference data, obtain the daily mean temperature from hourly data, compute the energy-consumption-related indices for the selected temporal aggregation (“DJF” for HDD and “JJA” for CDD), calculate the mean and trend over the historical period (1971-2000) and cache the result (to avoid redundant downloads and processing).
Show code cell source
Hide code cell source
transform_func_kwargs = {
"index_timeseries": dict(sorted(index_timeseries.items())),
"year_start": year_start,
"year_stop": year_stop,
}
ds_era5 = download.download_and_transform(
*request_era,
chunks=chunks,
transform_chunks=False,
transform_func=compute_indices_and_trends,
transform_func_kwargs=transform_func_kwargs | {"resample_reduction": "mean"},
)
2.2. Download and transform models#
In this section, the download.download_and_transform function from the ‘c3s_eqc_automatic_quality_control’ package is employed to download daily data from the CMIP6 models, compute the energy-consumption-related indices for the selected temporal aggregation (“DJF” for HDD and “JJA” for CDD), calculate the mean and trend over the historical period (1971-2000), interpolate to ERA5’s grid (only for the cases in which it is specified, in the other cases, the original model’s grid is mantained), and cache the result (to avoid redundant downloads and processing).
Show code cell source
Hide code cell source
interpolated_datasets = []
model_datasets = {}
for model, requests in model_requests.items():
print(f"{model=}")
model_kwargs = {
"chunks": chunks,
"transform_chunks": False,
"transform_func": compute_indices_and_trends,
}
# Original model
model_datasets[model] = download.download_and_transform(
*requests,
**model_kwargs,
transform_func_kwargs=transform_func_kwargs,
)
# Interpolated model
ds = download.download_and_transform(
*requests,
**model_kwargs,
transform_func_kwargs=transform_func_kwargs
| {
"request_grid_out": request_lsm,
"method": interpolation_method,
"skipna": True,
},
)
interpolated_datasets.append(ds.expand_dims(model=[model]))
ds_interpolated = xr.concat(interpolated_datasets, "model", coords='minimal', compat='override')
model='access_cm2'
model='awi_cm_1_1_mr'
model='cmcc_esm2'
model='cnrm_cm6_1_hr'
model='cnrm_esm2_1'
model='ec_earth3_cc'
model='gfdl_esm4'
model='inm_cm4_8'
model='inm_cm5_0'
model='kiost_esm'
model='mpi_esm1_2_lr'
model='miroc6'
model='miroc_es2l'
model='mri_esm2_0'
model='noresm2_mm'
model='nesm3'
2.3. Apply land-sea mask, change attributes and cut the region to show#
This section performs the following tasks:
Cut the region of interest.
Downloads the sea mask for ERA5.
Applies the sea mask to both ERA5 data and the model data, which were previously regridded to ERA5’s grid (i.e., it applies the ERA5 sea mask to
ds_interpolated).Regrids the ERA5 land-sea mask to the model’s grid and applies it to them.
Change some variable attributes for plotting purposes.
Note: ds_interpolated contains data from the models (mean and trend over the historical period, p-value of the trends…) regridded to ERA5. model_datasets contain the same data but in the original grid of each model.
Show code cell source
Hide code cell source
lsm = download.download_and_transform(*request_lsm)["lsm"].squeeze(drop=True)
# Cutout
regionalise_kwargs = {
"lon_slice": slice(area[1], area[3]),
"lat_slice": slice(area[0], area[2]),
}
lsm = utils.regionalise(lsm, **regionalise_kwargs)
ds_interpolated = utils.regionalise(ds_interpolated, **regionalise_kwargs)
model_datasets = {
model: utils.regionalise(ds, **regionalise_kwargs)
for model, ds in model_datasets.items()
}
# Mask
ds_era5 = ds_era5.where(lsm)
ds_interpolated = ds_interpolated.where(lsm)
model_datasets = {
model: ds.where(diagnostics.regrid(lsm, ds, method="bilinear"))
for model, ds in model_datasets.items()
}
# Edit attributes
for ds in (ds_era5, ds_interpolated, *model_datasets.values()):
ds["trend"] *= 10
ds["trend"].attrs = {"long_name": "trend"}
for index in index_timeseries:
ds[index].attrs = {"long_name": "", "units": "°C" if ds[index].attrs["units"]=="K"
else (ds[index].attrs["units"])}
3. Plot and describe results#
This section will display the following results:
Maps representing the spatial distribution of the historical mean values (1971-2000) of the indices ‘HDD15.5’ and ‘CDD22’ for ERA5, each model individually, the ensemble median (understood as the median of the mean values of the chosen subset of models calculated for each grid cell), and the ensemble spread (derived as the standard deviation of the distribution of the chosen subset of models).
Maps representing the spatial distribution of the historical trends (1971-2000) of the considered indices. Similar to the first analysis, this includes ERA5, each model individually, the ensemble median (understood as the median of the trend values of the chosen subset of models calculated for each grid cell), and the ensemble spread (derived as the standard deviation of the distribution of the chosen subset of models).
Bias maps of the historical mean values.
Trend bias maps.
Boxplots representing statistical distributions (PDF) built on the spatially-averaged historical trends from each considered model, displayed together with ERA5.
3.1. Define plotting functions#
The functions presented here are used to plot the mean values and trends calculated over the historical period (1971-2000) for each of the indices (‘HDD15.5’ and ‘CDD22’).
For a selected index, three layout types can be displayed, depending on the chosen function:
Layout including the reference ERA5 product, the ensemble median, the bias of the ensemble median, and the ensemble spread:
plot_ensemble()is used.Layout including every model (for the trend and mean values):
plot_models()is employed.Layout including the bias of every model (for the trend and mean values):
plot_models()is used again.
trend==True argument allows displaying trend values over the historical period, while trend==False will show mean values. When the trend argument is set to True, regions with no significance are hatched. For individual models and ERA5, a grid point is considered to have a statistically significant trend when the p-value is lower than 0.05 (in such cases, no hatching is shown). However, for determining trend significance for the ensemble median (understood as the median of the trend values of the chosen subset of models calculated for each grid cell), reliance is placed on agreement categories, following the advanced approach proposed in AR6 IPCC on pages 1945-1950. The hatch_p_value_ensemble() function is used to distinguish, for each grid point, between three possible cases:
If more than 66% of the models are statistically significant (p-value < 0.05) and more than 80% of the models share the same sign, we consider the ensemble median trend to be statistically significant, and there is agreement on the sign. To represent this, no hatching is used.
If less than 66% of the models are statistically significant, regardless of agreement on the sign of the trend, hatching is applied (indicating that the ensemble median trend is not statistically significant).
If more than 66% of the models are statistically significant but less than 80% of the models share the same sign, we consider the ensemble median trend to be statistically significant, but there is no agreement on the sign of the trend. This is represented using crosses.
Show code cell source
Hide code cell source
#Define function to plot the caption of the figures (for the ensemble case)
def add_caption_ensemble(trend,exp,index):
#Add caption to the figure
match trend:
case True:
caption_text= (
f"Fig {fig_number}. {long_name[index]} ('{index}') for "
f"the temporal aggreggtion of '{index_timeseries[index]}'. Trend for "
f"the {exp} period ({year_start} - {year_stop}). The layout "
f"includes data corresponding to: (a) ERA5, (b) the ensemble median "
f"(understood as the median of the trend values of the chosen subset of models "
f"calculated for each grid cell), "
f"(c) the bias of the ensemble median and (d) the ensemble spread "
f"(derived as the standard deviation of the distribution of the chosen "
f"subset of models)."
)
case False:
caption_text= (
f"Fig {fig_number}. {long_name[index]} ('{index}') for "
f"the temporal aggreggtion of '{index_timeseries[index]}'. Mean for "
f"the {exp} period ({year_start} - {year_stop}). The layout "
f"includes data corresponding to: (a) ERA5, (b) the ensemble median "
f"(understood as the median of the mean values of the chosen subset of models "
f"calculated for each grid cell), "
f"(c) the bias of the ensemble median and (d) the ensemble spread "
f"(derived as the standard deviation of the distribution of the chosen "
f"subset of models)."
)
wrapped_lines = textwrap.wrap(caption_text, width=105)
# Add each line to the figure
for i, line in enumerate(wrapped_lines):
fig.text(0, -0.05 - i * 0.03, line, ha='left', fontsize=10)
#end captioning
#Define function to plot the caption of the figures (for the individual models case)
def add_caption_models(trend,bias,exp,index):
#Add caption to the figure
if bias:
match trend:
case True:
caption_text = (
f"Fig {fig_number}. {long_name[index]} ('{index}') for the "
f"temporal aggregation of '{index_timeseries[index]}'. Trend bias for the "
f"{exp} period ({year_start} - {year_stop}) of each individual "
f"{collection_id} model."
)
case False:
caption_text = (
f"Fig {fig_number}. {long_name[index]} ('{index}') for the "
f"temporal aggreggtion of '{index_timeseries[index]}'. Mean bias for the "
f"{exp} period ({year_start} - {year_stop}) of each individual "
f"{collection_id} model."
)
else:
match trend:
case True:
caption_text = (
f"Fig {fig_number}. {long_name[index]} ('{index}') for the "
f"temporal aggreggtion of '{index_timeseries[index]}'. Trend for the {exp} "
f"period ({year_start} - {year_stop}) of each individual "
f"{collection_id} model."
)
case False:
caption_text = (
f" Fig {fig_number}. {long_name[index]} ('{index}') for the "
f"temporal aggreggtion of '{index_timeseries[index]}'. Mean for the {exp} "
f"period ({year_start} - {year_stop}) of each individual "
f"{collection_id} model."
)
wrapped_lines = textwrap.wrap(caption_text, width=120)
# Add each line to the figure
for i, line in enumerate(wrapped_lines):
fig.text(0, -0.05 - i * 0.03, line, ha='left', fontsize=10)
def hatch_p_value(da, ax, **kwargs):
default_kwargs = {
"plot_func": "contourf",
"show_stats": False,
"cmap": "none",
"add_colorbar": False,
"levels": [0, 0.05, 1],
"hatches": ["", "/" * 3],
}
kwargs = default_kwargs | kwargs
title = ax.get_title()
plot_obj = plot.projected_map(da, ax=ax, **kwargs)
ax.set_title(title)
return plot_obj
def hatch_p_value_ensemble(trend, p_value, ax):
n_models = trend.sizes["model"]
robust_ratio = (p_value <= 0.05).sum("model") / n_models
robust_ratio = robust_ratio.where(p_value.notnull().any("model"))
signs = xr.concat([(trend > 0).sum("model"), (trend < 0).sum("model")], "sign")
sign_ratio = signs.max("sign") / n_models
robust_threshold = 0.66
sign_ratio = sign_ratio.where(robust_ratio > robust_threshold)
for da, threshold, character in zip(
[robust_ratio, sign_ratio], [robust_threshold, 0.8], ["/", "\\"]
):
hatch_p_value(da, ax=ax, levels=[0, threshold, 1], hatches=[character * 3, ""])
def set_extent(da, axs, area):
extent = [area[i] for i in (1, 3, 2, 0)]
for i, coord in enumerate(extent):
extent[i] += -1 if i % 2 else +1
for ax in axs:
ax.set_extent(extent)
def plot_models(
data,
da_for_kwargs=None,
p_values=None,
col_wrap=4,
subplot_kw={"projection": ccrs.PlateCarree()},
figsize=None,
layout="constrained",
area=area,
**kwargs,
):
if isinstance(data, dict):
assert da_for_kwargs is not None
model_dataarrays = data
else:
da_for_kwargs = da_for_kwargs or data
model_dataarrays = dict(data.groupby("model"))
if p_values is not None:
model_p_dataarrays = (
p_values if isinstance(p_values, dict) else dict(p_values.groupby("model"))
)
else:
model_p_dataarrays = None
# Get kwargs
default_kwargs = {"robust": True, "extend": "both"}
kwargs = default_kwargs | kwargs
kwargs = xr.plot.utils._determine_cmap_params(da_for_kwargs.values, **kwargs)
fig, axs = plt.subplots(
*(col_wrap, math.ceil(len(model_dataarrays) / col_wrap)),
subplot_kw=subplot_kw,
figsize=figsize,
layout=layout,
)
axs = axs.flatten()
for (model, da), ax in zip(model_dataarrays.items(), axs):
pcm = plot.projected_map(
da, ax=ax, show_stats=False, add_colorbar=False, **kwargs
)
ax.set_title(model)
if model_p_dataarrays is not None:
hatch_p_value(model_p_dataarrays[model], ax)
set_extent(da_for_kwargs, axs, area)
fig.colorbar(
pcm,
ax=axs.flatten(),
extend=kwargs["extend"],
location="right",
label=f"{da_for_kwargs.attrs.get('long_name', '')} [{da_for_kwargs.attrs.get('units', '')}]",
)
return fig
def plot_ensemble(
da_models,
da_era5=None,
p_value_era5=None,
p_value_models=None,
subplot_kw={"projection": ccrs.PlateCarree()},
figsize=None,
layout="constrained",
cbar_kwargs=None,
area=area,
cmap_bias=None,
cmap_std=None,
**kwargs,
):
# Get kwargs
default_kwargs = {"robust": True, "extend": "both"}
kwargs = default_kwargs | kwargs
kwargs = xr.plot.utils._determine_cmap_params(
da_models.values if da_era5 is None else da_era5.values, **kwargs
)
if da_era5 is None and cbar_kwargs is None:
cbar_kwargs = {"orientation": "horizontal"}
# Figure
fig, axs = plt.subplots(
*(1 if da_era5 is None else 2, 2),
subplot_kw=subplot_kw,
figsize=figsize,
layout=layout,
)
axs = axs.flatten()
axs_iter = iter(axs)
# ERA5
if da_era5 is not None:
ax = next(axs_iter)
plot.projected_map(
da_era5, ax=ax, show_stats=False, cbar_kwargs=cbar_kwargs, **kwargs
)
if p_value_era5 is not None:
hatch_p_value(p_value_era5, ax=ax)
ax.set_title("(a) ERA5")
# Median
ax = next(axs_iter)
median = da_models.median("model", keep_attrs=True)
plot.projected_map(
median, ax=ax, show_stats=False, cbar_kwargs=cbar_kwargs, **kwargs
)
if p_value_models is not None:
hatch_p_value_ensemble(trend=da_models, p_value=p_value_models, ax=ax)
ax.set_title("(b) Ensemble Median" if da_era5 is not None else "(a) Ensemble Median")
# Bias
if da_era5 is not None:
ax = next(axs_iter)
with xr.set_options(keep_attrs=True):
bias = median - da_era5
plot.projected_map(
bias,
ax=ax,
show_stats=False,
center=0,
cbar_kwargs=cbar_kwargs,
**(default_kwargs | {"cmap": cmap_bias}),
)
ax.set_title("(c) Ensemble Median Bias")
# Std
ax = next(axs_iter)
std = da_models.std("model", keep_attrs=True)
plot.projected_map(
std,
ax=ax,
show_stats=False,
cbar_kwargs=cbar_kwargs,
**(default_kwargs | {"cmap": cmap_std}),
)
ax.set_title("(d) Ensemble Standard Deviation" if da_era5 is not None else "(b) Ensemble Standard Deviation")
set_extent(da_models, axs, area)
return fig
The colorbar chosen for representing biases and trends for the HDD15.5 index ranges from red to blue. In this color scheme, negative bias values (red colors) indicate that the Heating Degree Days displayed by the models are lower than those shown by ERA5. Similarly, negative trend values (red colors) indicate a decrease in Heating Degree Days over time. Instead, blueish colors denote more Heating Degree Days, either indicating a positive bias compared to ERA5 or an increase in Heating Degree Days over time. This selection is based on the rationale that more Heating Degree Days are associated with colder conditions, typically represented by blueish colors, while fewer Heating Degree Days imply warmer conditions, depicted by reddish colors.
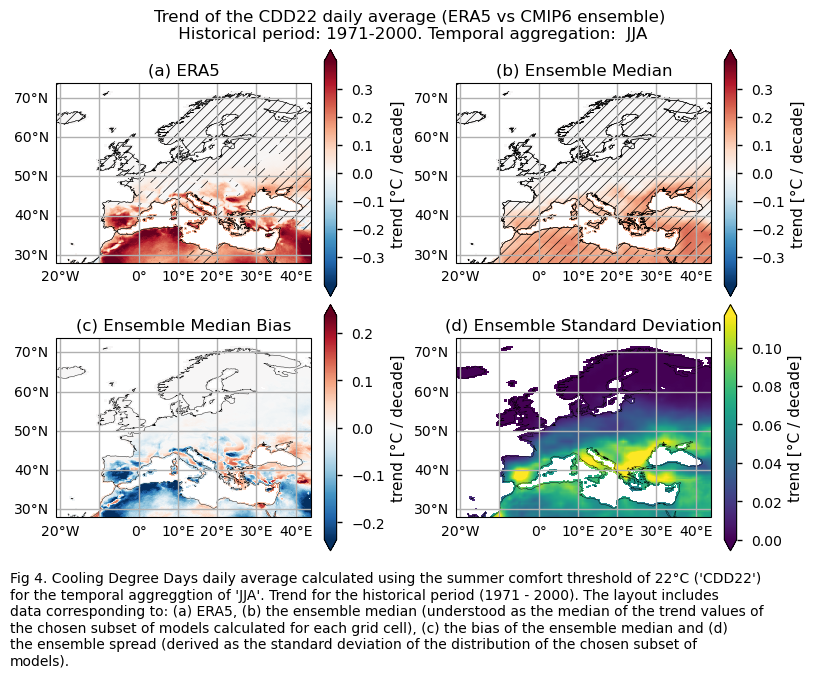
3.2. Plot ensemble maps#
In this section, we invoke the plot_ensemble() function to visualise the mean values and trends calculated over the historical period (1971-2000) for the model ensemble and ERA5 reference product across Europe. Note that the model data used in this section has previously been interpolated to the ERA5 grid.
Specifically, for each of the indices (‘HDD15.5’ and ‘CDD22’), this section presents two layouts:
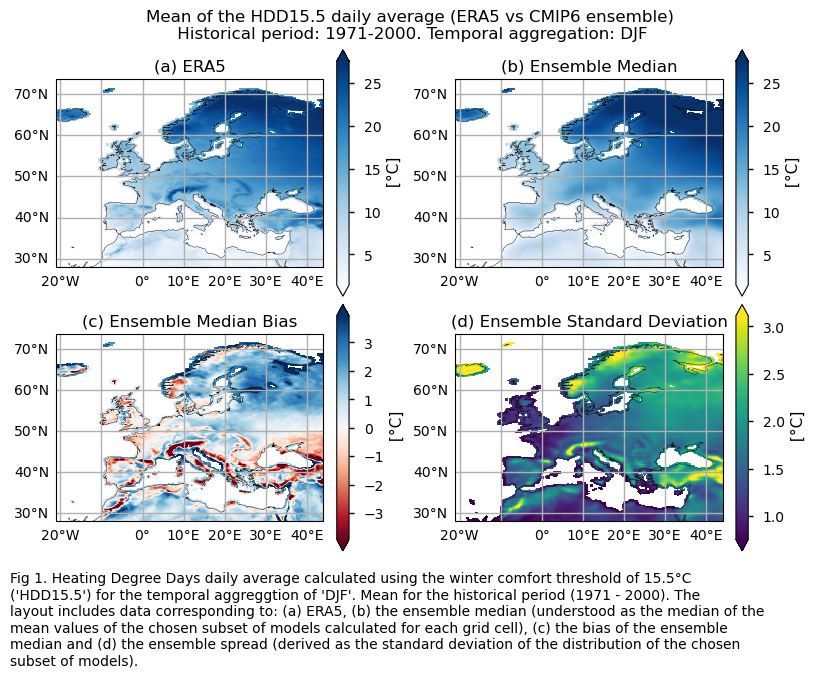
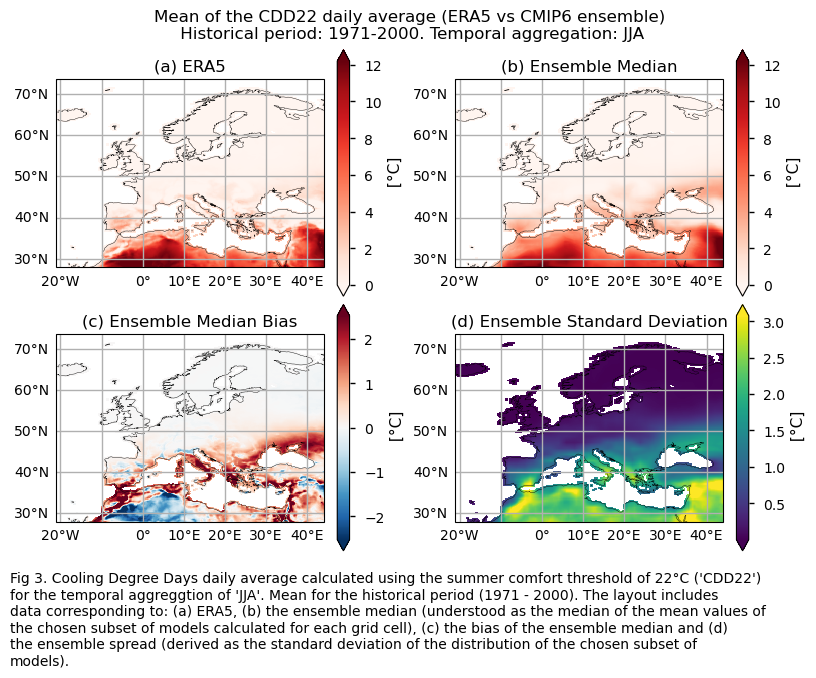
Mean values of the historical period (1971-2000) for: (a) the reference ERA5 product, (b) the ensemble median (understood as the median of the mean values of the chosen subset of models calculated for each grid cell), (c) the bias of the ensemble median, and (d) the ensemble spread (derived as the standard deviation of the distribution of the chosen subset of models).
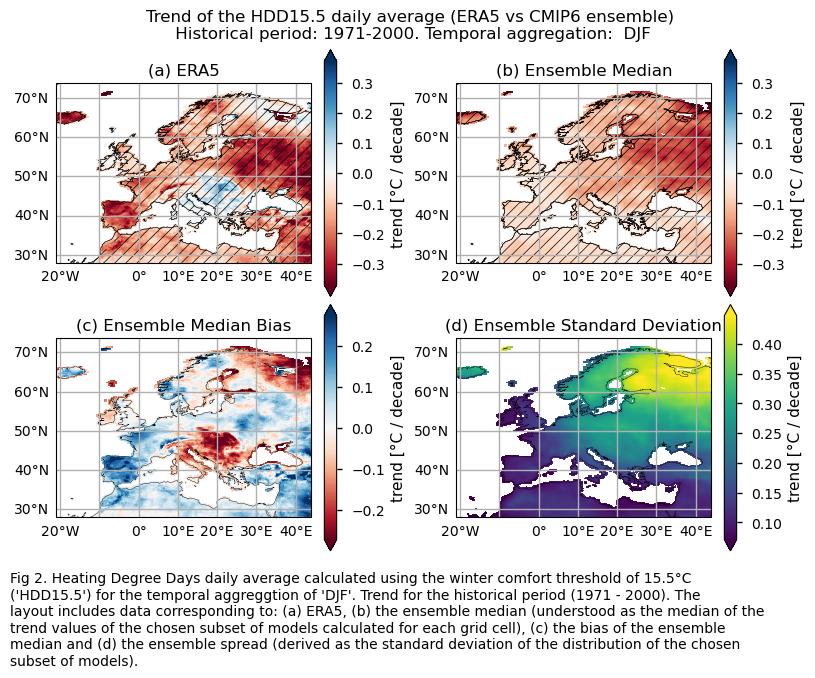
Trend values of the historical period (1971-2000) for: (a) the reference ERA5 product, (b) the ensemble median (understood as the median of the trend values of the chosen subset of models calculated for each grid cell), (c) the bias of the ensemble median, and (d) the ensemble spread (derived as the standard deviation of the distribution of the chosen subset of models).
Show code cell source
Hide code cell source
#Fig number counter
fig_number=1
#Common title
common_title = f"Historical period: {year_start}-{year_stop}. Temporal aggregation: "
for index in index_timeseries:
# Index
da = ds_interpolated[index]
fig = plot_ensemble(
da_models=da,
da_era5=ds_era5[index],
cmap=cmaps.get(index),
cmap_bias=cmaps_bias.get(index),
)
fig.suptitle(f"Mean of the {index} daily average (ERA5 vs {collection_id} ensemble)\n {common_title}{index_timeseries[index]}")
add_caption_ensemble(trend=False,exp="historical",index=index)
plt.show()
fig_number=fig_number+1
print(f"\n")
# Trend
da_era5_trend = ds_era5["trend"].sel(index=index)
da_era5_trend.attrs["units"] = f"{da.attrs['units']} / decade"
da_trend = ds_interpolated["trend"].sel(index=index)
da_trend.attrs["units"] = f"{da.attrs['units']} / decade"
fig = plot_ensemble(
da_models=da_trend,
da_era5=da_era5_trend,
p_value_era5=ds_era5["p"].sel(index=index),
p_value_models=ds_interpolated["p"].sel(index=index),
center=0,
cmap=cmaps_trend.get(index),
cmap_bias=cmaps_bias.get(index),
)
fig.suptitle(f"Trend of the {index} daily average (ERA5 vs {collection_id} ensemble)\n {common_title} {index_timeseries[index]}")
add_caption_ensemble(trend=True,exp="historical",index=index)
plt.show()
fig_number=fig_number+1
print(f"\n")
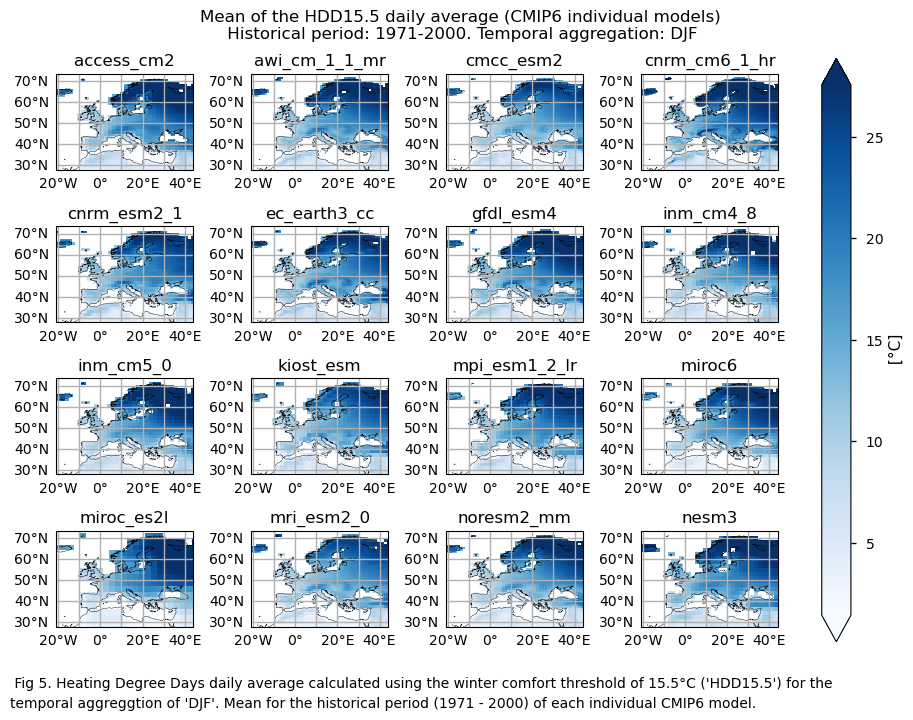
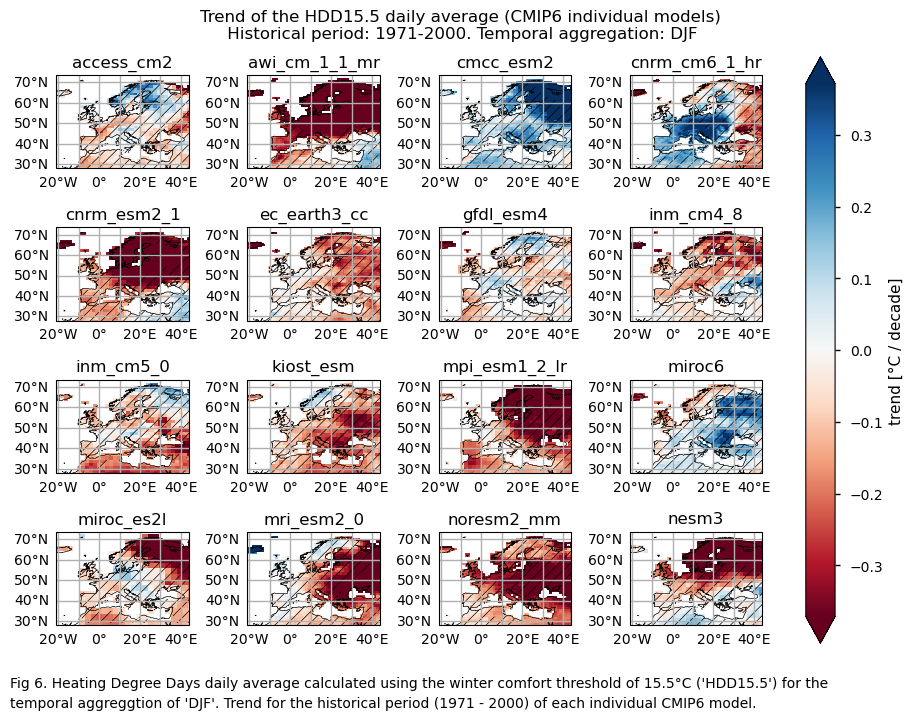
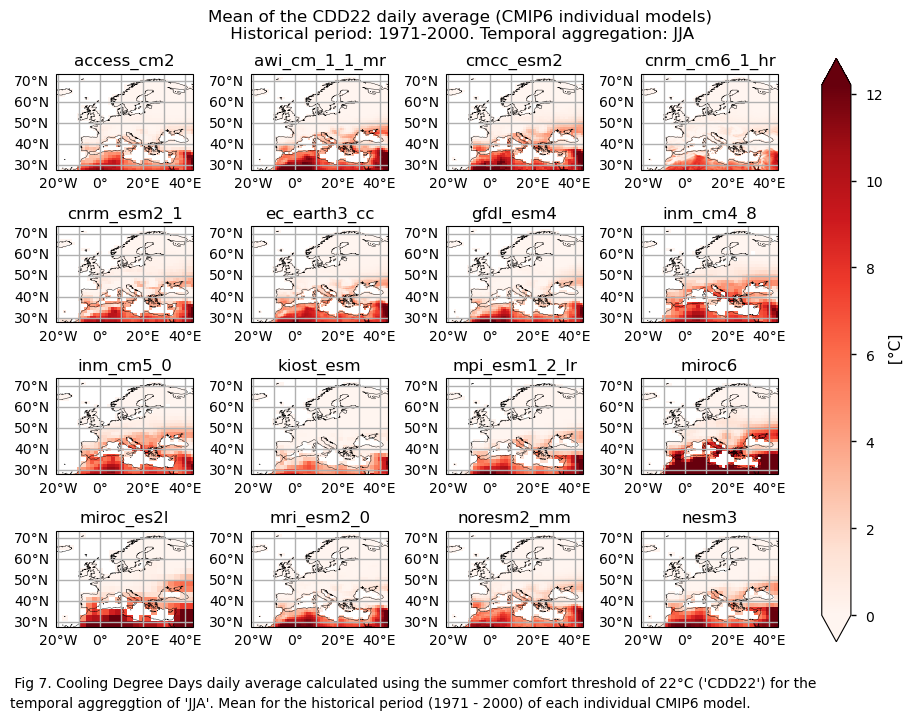
3.3. Plot model maps#
In this section, we invoke the plot_models() function to visualise the mean values and trends calculated over the historical period (1971-2000) for every model individually across Europe. Note that the model data used in this section maintains its original grid.
Specifically, for each of the indices (‘HDD15.5’ and ‘CDD22’), this section presents two layouts:
A layout including the historical mean (1971-2000) of every model.
A layout including the historical trend (1971-2000) of every model.
Show code cell source
Hide code cell source
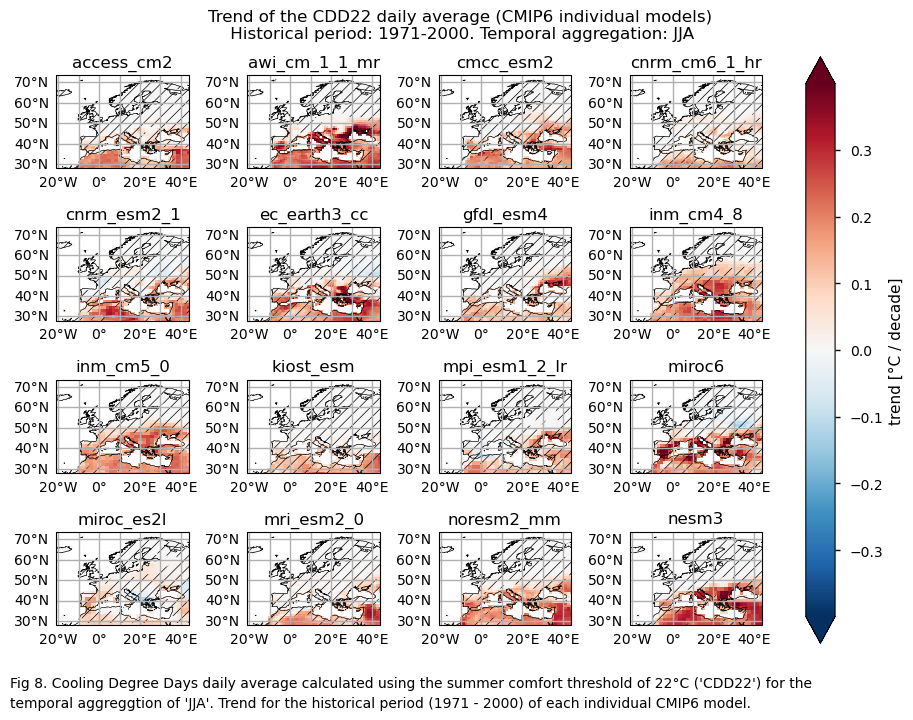
for index in index_timeseries:
# Index
da_for_kwargs = ds_era5[index]
fig = plot_models(
data={model: ds[index] for model, ds in model_datasets.items()},
da_for_kwargs=da_for_kwargs,
figsize=[9,6.5],
cmap=cmaps.get(index),
)
fig.suptitle(f"Mean of the {index} daily average ({collection_id} individual models)\n {common_title}{index_timeseries[index]}")
add_caption_models(trend=False,bias=False,exp="historical",index=index)
plt.show()
print(f"\n")
fig_number=fig_number+1
# Trend
da_for_kwargs_trends = ds_era5["trend"].sel(index=index)
da_for_kwargs_trends.attrs["units"] = f"{da_for_kwargs.attrs['units']} / decade"
fig = plot_models(
data={
model: ds["trend"].sel(index=index) for model, ds in model_datasets.items()
},
da_for_kwargs=da_for_kwargs_trends,
p_values={
model: ds["p"].sel(index=index) for model, ds in model_datasets.items()
},
center=0,
figsize=[9,6.5],
cmap=cmaps_trend.get(index),
)
fig.suptitle(f"Trend of the {index} daily average ({collection_id} individual models)\n {common_title}{index_timeseries[index]}")
add_caption_models(trend=True,bias=False,exp="historical",index=index)
plt.show()
print(f"\n")
fig_number=fig_number+1
3.4. Plot bias maps#
In this section, we invoke the plot_models() function to visualise the bias for the mean values and trends calculated over the historical period (1971-2000) for every model individually across Europe. Note that the model data used in this section has previously been interpolated to the ERA5 grid.
Specifically, for each of the indices (‘HDD15.5’ and ‘CDD22’), this section presents two layouts:
A layout including the bias for the historical mean (1971-2000) of every model.
A layout including the bias for the historical trend (1971-2000) of every model.
Show code cell source
Hide code cell source
with xr.set_options(keep_attrs=True):
bias = ds_interpolated - ds_era5
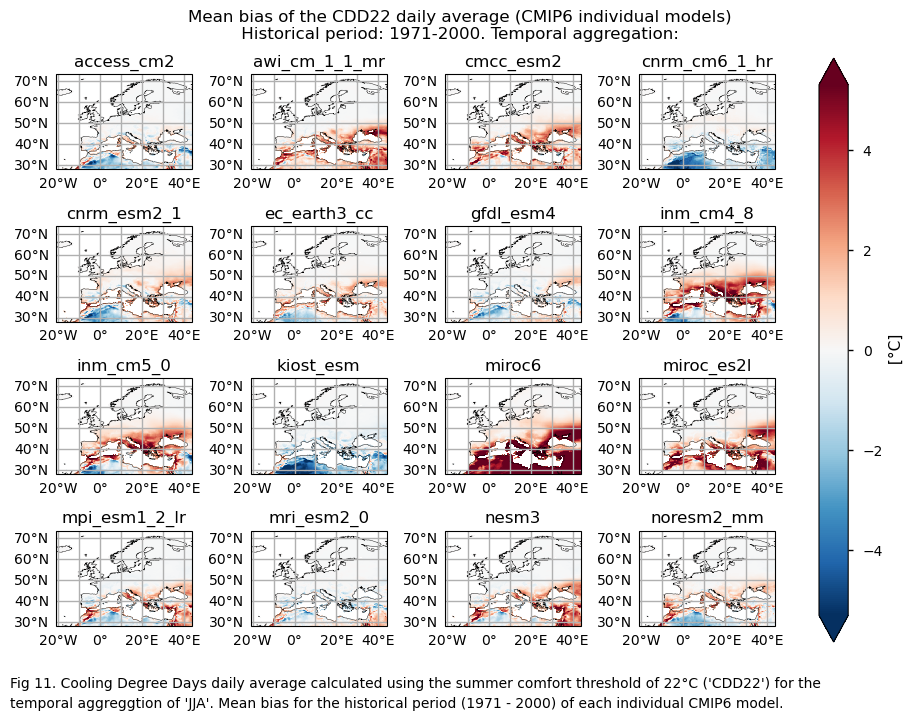
for index in index_timeseries:
# Index bias
da = bias[index]
fig = plot_models(data=da, center=0, cmap=cmaps_bias.get(index),figsize=[9,6.5])
fig.suptitle(f"Mean bias of the {index} daily average ({collection_id} individual models)\n {common_title}")
add_caption_models(trend=False,bias=True,exp="historical",index=index)
plt.show()
print(f"\n")
fig_number=fig_number+1
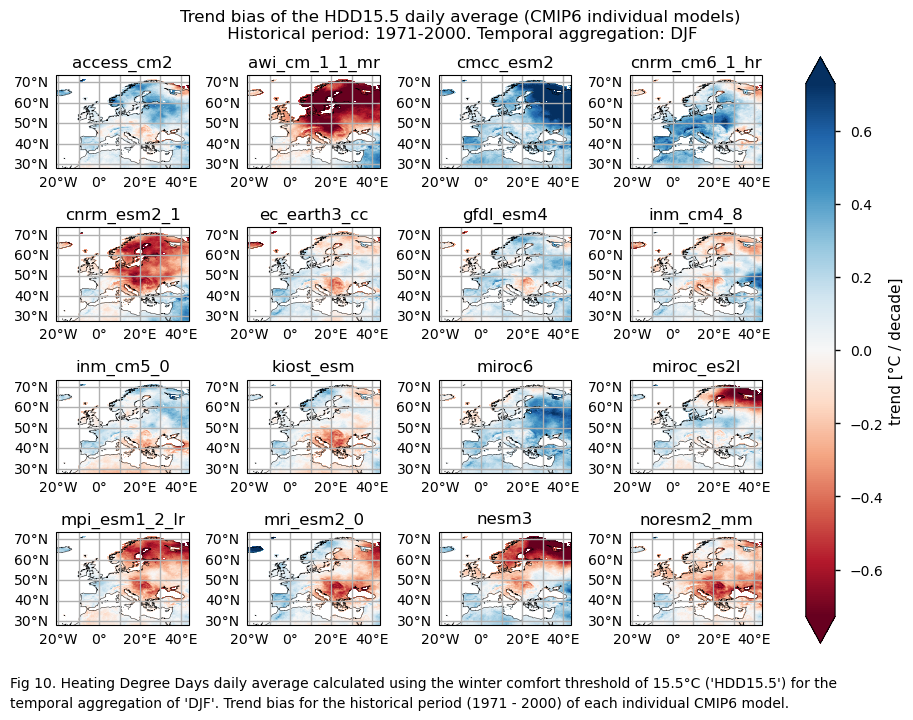
# Trend bias
da_trend = bias["trend"].sel(index=index)
da_trend.attrs["units"] = f"{da.attrs['units']} / decade"
fig = plot_models(data=da_trend, center=0, cmap=cmaps_bias.get(index),figsize=[9,6.5])
fig.suptitle(f"Trend bias of the {index} daily average ({collection_id} individual models)\n {common_title}{index_timeseries[index]}")
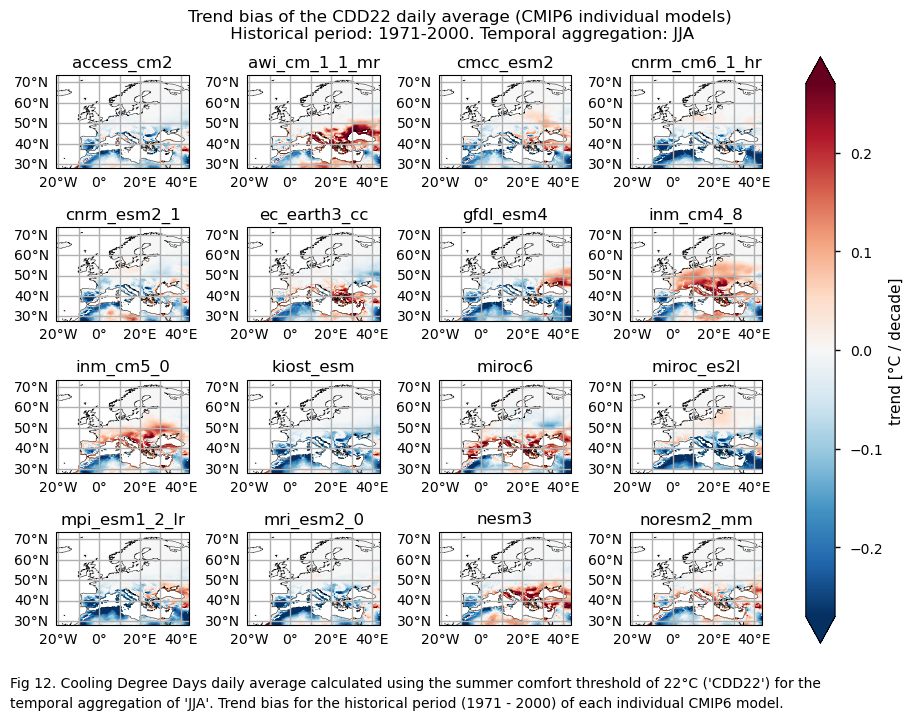
add_caption_models(trend=True,bias=True,exp="historical",index=index)
plt.show()
print(f"\n")
fig_number=fig_number+1
plt.show()
3.5. Boxplots of the historical trend#
In this last section, we compare the trends of the climate models with the reference trend from ERA5.
Dots represent the spatially-averaged historical trend over the selected region (change of the number of days per decade) for each model (grey), the ensemble mean (blue), and the reference product (orange). The ensemble median is shown as a green line. Note that the spatially averaged values are calculated for each model from its original grid (i.e., no interpolated data has been used here).
The boxplot visually illustrates the distribution of trends among the climate models, with the box covering the first quartile (Q1 = 25th percentile) to the third quartile (Q3 = 75th percentile), and a green line indicating the ensemble median (Q2 = 50th percentile). Whiskers extend from the edges of the box to show the full data range.
Show code cell source
Hide code cell source
weights = collection_id == "CMIP6"
mean_datasets = [
diagnostics.spatial_weighted_mean(ds.expand_dims(model=[model]), weights=weights)
for model, ds in model_datasets.items()
]
mean_ds = xr.concat(mean_datasets, "model", coords='minimal',compat='override')
index_str=1
for index, da in mean_ds["trend"].groupby("index"):
df_slope = da.to_dataframe()[["trend"]]
ax = df_slope.boxplot()
ax.scatter(
x=[1] * len(df_slope),
y=df_slope,
color="grey",
marker=".",
label="models",
)
# Ensemble mean
ax.scatter(
x=1,
y=da.mean("model"),
marker="o",
label=f"{collection_id} Ensemble Mean",
)
# ERA5
labels = [f"{collection_id} Ensemble"]
da = ds_era5["trend"].sel(index=index)
da = diagnostics.spatial_weighted_mean(da)
ax.scatter(
x=2,
y=da.values,
marker="o",
label="ERA5",
)
labels.append("ERA5")
ax.set_xticks(range(1, len(labels) + 1), labels)
ax.set_ylabel(f"{ds[index].attrs['units']} / decade")
plt.suptitle(
f"({chr(ord('`')+index_str)}) Trend of {index} \n"
f"region: lon [{-area[1]}W, {area[3]}E] x lat [{area[2]}N, {area[0]}N] \n"
f"period: {year_start}-{year_stop}. Temporal aggregation: {index_timeseries[index]}"
)
plt.legend()
plt.show()
index_str=index_str+1
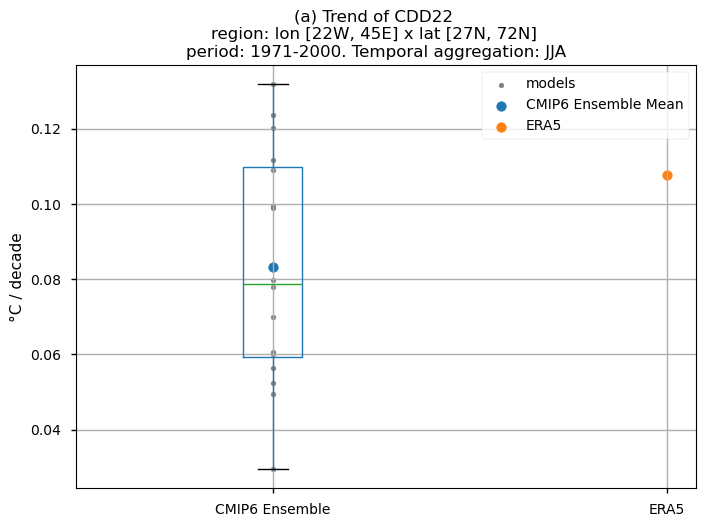
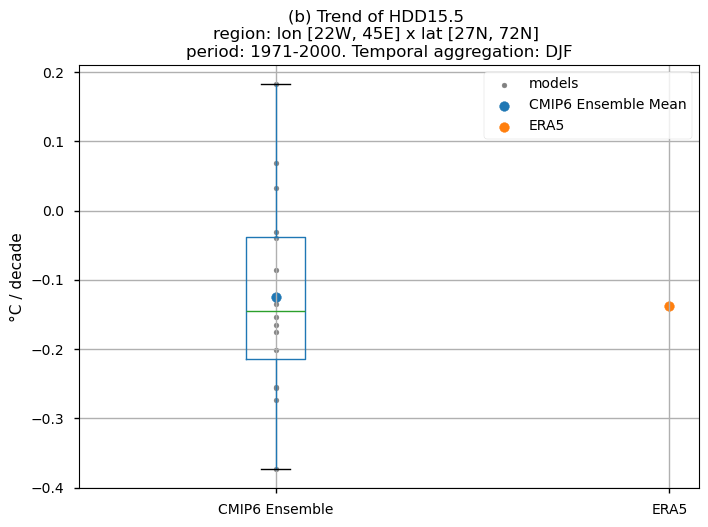
Fig 13. Boxplots illustrating the historical trends of the distribution of the chosen subset of models and ERA5 for the Energy Degree Days indices daily averaged: (a) 'CDD22', and (b) 'HDD15.5'. The distribution is created by considering spatially averaged trends across Europe. The ensemble mean and the ensemble median trends are both included. Outliers in the distribution are denoted by a grey circle with a black contour.
3.6. Results summary and discussion#
GCMs struggle to accurately represent the climatology of these indices in regions with complex orography, specially for the mean values of the HDD15.5 index. There is a common overestimation of HDD15.5 mean values for DJF, especially in continental and northern areas. Conversely, underestimation is evident in mountainous regions and in some western zones. For the climatological values of CDD22, there is overestimation for JJA across most of the Mediterranean Basin (except some Saharan regions).
The ERA5 historical data shows a reduction in Heating Degree Days (HDD) for DJF across most of Europe. However, while the ensemble median of GCMs (calculated for each grid cell) captures the trend behavior for most regions, it does not accurately reflect their magnitude. Indeed, a significant inter-model spread is evident, with differences in trend direction among individual models observed in some regions. This variability is particularly pronounced in the northern and northeastern parts of Europe.
The ERA5 historical trend shows an increase in Cooling Degree Days during the summer (JJA) across Europe, especially in the Mediterranean Basin. GCMs agree on the direction of the CDD2 trend for summer and replicate the historical trends (1971-2000) of the selected index, although they underestimate its magnitude.
Boxplots reveal different signs for the spatial-averaged historical trend characterising the distribution of the chosen subset of models for the HDD15.5 and DJF. The CMIP6 ensemble median trend displays a daily average value around -0.15 °C/10 years, similar to ERA5’s -0.15 °C/10 years. The interquantile range of the ensemble ranges from below -0.2 to near -0.05 °C per decade. When assessing the biases of the trend, it can be seen that the interquantile range of the ensemble for the trend bias goes approximately from -0.1 to 0.1 °C per decade.
Boxplots exhibit a consistent positive spatial-averaged historical trend characterising the different models for the CDD22 for JJA. Magnitudes, however, are slightly underestimated when compared to ERA5. The CMIP6 ensemble median displays near 0.08°C/10 years, contrasting with ERA5’s ~0.11 °C/10 years. The interquantile range of the ensemble ranges from 0.06 to 0.11 °C per decade. The interquantile range of the ensemble for the trend bias goes approximately from -0.05 to slightly above 0°C per decade.
What do the results mean for users? Are the biases relevant?
Despite the biases and high inter-model spread in some regions, the outcomes of this notebook may offer valuable insights for decisions sensitive to future energy demand. These results, particularly for CDD22 calculated for summer, may increase confidence in using these models to analyse future trends, although their accuracy is not guaranteed. To improve the accuracy of these insights, biases should be considered and corrected [6][7].
It is important to note that the results presented are specific to the 16 models chosen, and users should aim to assess as wide a range of models as possible before making a sub-selection.
ℹ️ If you want to know more#
Key resources#
Some key resources and further reading were linked throughout this assessment.
The CDS catalogue entries for the data used were:
CMIP6 climate projections (Daily - air temperature): https://cds.climate.copernicus.eu/datasets/projections-cmip6?tab=overview
ERA5 hourly data on single levels from 1940 to present (2m temperature): https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels?tab=overview
Code libraries used:
C3S EQC custom functions,
c3s_eqc_automatic_quality_control, prepared by B-Openicclim Python package
References#
[1] Bindi, M., Olesen, J.E. The responses of agriculture in Europe to climate change (2011). Reg Environ Change 11 (Suppl 1), 151–158. https://doi.org/10.1007/s10113-010-0173-x
[2] Lindner, M., Maroschek, M., Netherer, S., Kremer, A., Barbati, A., Garcia-Gonzalo, J., Seidi, R., Delzon, S., Corona, P., Kolstrom, M., Lexer, M.J., Marchetti, M. (2010). Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. For. Ecol. Manage. 259(4): 698–709. https://doi.org/10.1016/j.foreco.2009.09.023
[3] Santamouris, M., Cartalis, C., Synnefa, A., Kolokotsa, D. (2015). On the impact of urban heat island and global warming on the power demand and electricity consumption of buildings – a review. Energy Build. 98: 119–124. https://doi.org/10.1016/j.enbuild.2014.09.052
[4] Jacob, D., Petersen, J., Eggert, B. et al. (2014). EURO-CORDEX: new high-resolution climate change projections for European impact research. Reg Environ Change 14, 563–578. https://doi.org/10.1007/s10113-013-0499-2
[5] IPCC. 2014. In Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Core Writing Team, RK Pachauri, LA Meyer (eds). IPCC: Geneva, Switzerland 151 pp.
[6] Spinoni, J., Vogt, J.V., Barbosa, P., Dosio, A., McCormick, N., Bigano, A. and Füssel, H.-M. (2018). Changes of heating and cooling degree-days in Europe from 1981 to 2100. Int. J. Climatol, 38: e191-e208. https://doi.org/10.1002/joc.5362
[7] Deroubaix, A., Labuhn, I., Camredon, M. et al. (2021). Large uncertainties in trends of energy demand for heating and cooling under climate change. Nat Commun 12, 5197. https://doi.org/10.1038/s41467-021-25504-8
[8] Scoccimarro, E., Cattaneo, O., Gualdi, S. et al. (2023). Country-level energy demand for cooling has increased over the past two decades. Commun Earth Environ 4, 208. https://doi.org/10.1038/s43247-023-00878-3
