CORDEX temperature biases over the Alpine region — assessment using E-OBS and CERRA

5.2.6. CORDEX temperature biases over the Alpine region — assessment using E-OBS and CERRA#

Production date: 30-06-2025

Produced by: CMCC foundation - Euro-Mediterranean Center on Climate Change. Albert Martinez Boti and Lorenzo Sangelantoni.

🌍 Use case: Investigating climate biases in mountain regions to inform the ski and hydrological sectors.#

❓ Quality assessment question#

Are the cold biases commonly found in Regional Climate Models over the Alps apparent when evaluated against CERRA?
Does applying a lapse-rate correction reduce these biases?

Mountains, although covering a limited land area, are vital to the global water cycle, acting as key sources of freshwater for both ecological and human needs [1]. In many mountainous regions, temperature is a critical driver of hydrometeorological processes such as the ratio of rain to snow, the timing of snowmelt, and the frequency of low-flow conditions [2]. These sensitivities make mountain regions key indicators of climate change. However, accurately representing temperature in complex terrain remains challenging for models due to factors like topographic variability, slope orientation, terrain shading, snow–albedo feedbacks, and vegetation heterogeneity [2]).

A recent literature-based quality assessment, CORDEX temperature biases over the Alpine region for the ski and hydrological sectors, synthesised multiple studies and confirmed that Regional Climate Models (RCMs) exhibit persistent cold biases over the Alps despite their relatively high resolution and improved representation of physical processes in mountainous terrain. Given that bias estimates are sensitive to the choice of reference dataset -as highlighted in the quality assessment [3][4]- here we evaluate RCM biases against E-OBS and include CERRA, a high-resolution (5.5 km) regional reanalysis produced using the HARMONIE-ALADIN limited-area numerical weather prediction and data assimilation system. The analysis includes a broad ensemble of EURO-CORDEX models and examines the altitude dependency of biases by evaluating results across different elevation bands. Finally, we apply a lapse-rate correction to place all datasets at a common elevation and investigate whether this influences the estimated biases.

📢 Quality assessment statement#

These are the key outcomes of this assessment

CORDEX simulations exhibit biases relative to both reference datasets (E-OBS and CERRA).
RCMs’ systematic cold biases above 1000–1500 m, reported in the literature, are evident when evaluated against E-OBS.
CORDEX biases relative to CERRA are weaker and show no systematic increase with altitude, unlike the case with E-OBS.
Large inter-model spread—especially for winter cold extremes above 1500 m—highlights significant uncertainty in representing conditions critical for alpine risk assessments.
Lapse-rate correction might slightly reduce biases by ensuring no elevation differences exist between datasets, but it does not fundamentally change the shape of vertical bias profiles or address the underlying model or observational issues driving the biases.
The findings of this Alpine-focused assessment highlight the need for caution when interpreting future temperature projections from RCMs. A central concern is the potential for present-climate biases to persist or propagate into future warming scenarios—an aspect that remains largely underexplored.

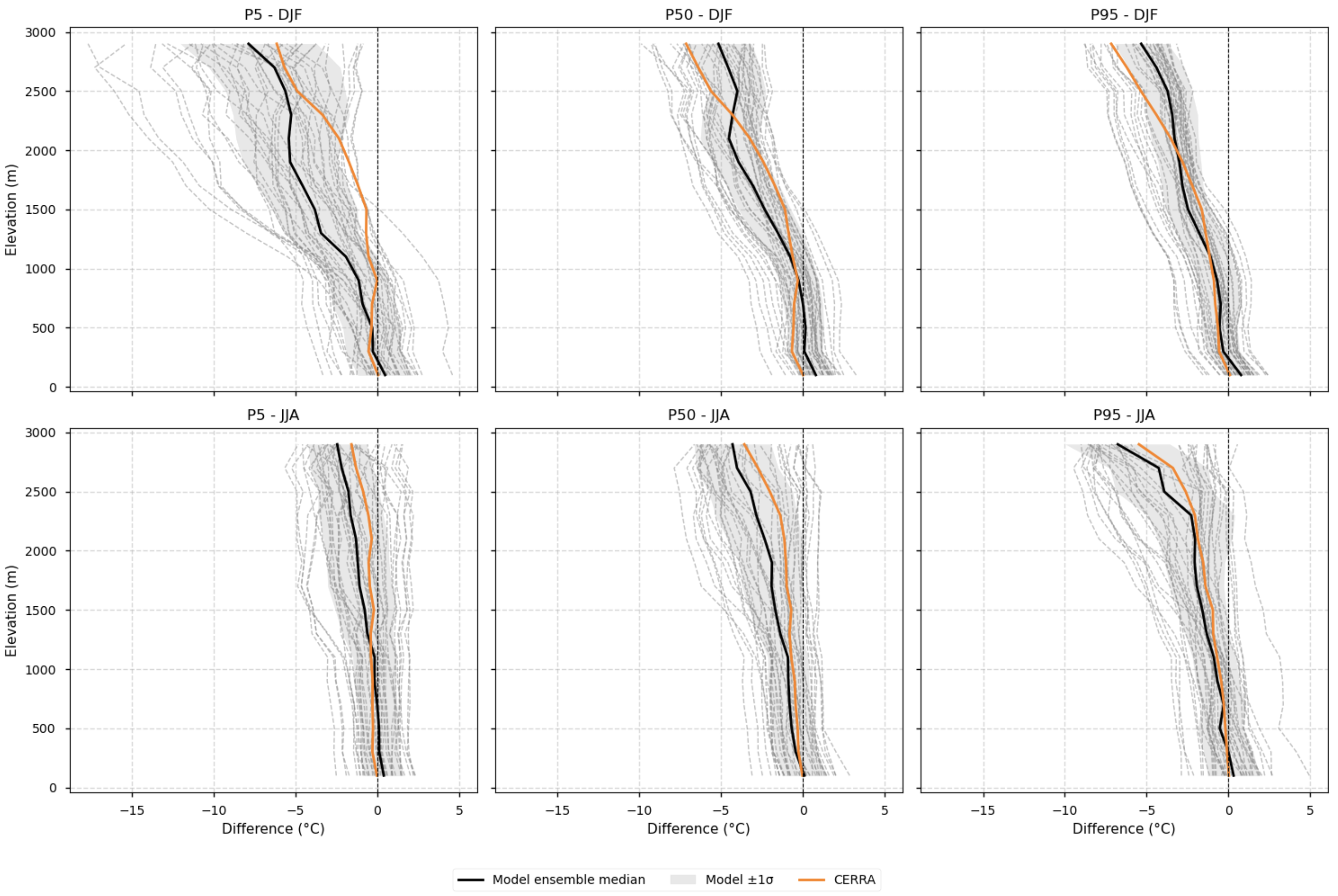
Visual abstract — Fig. 5.2.6.1 Elevation profiles of biases relative to E-OBS. Differences compared to the E-OBS vertical profile are shown for each EURO-CORDEX model individually, the ensemble median, the spread (calculated as the standard deviation), and CERRA. Profiles are plotted separately for winter (DJF) and summer (JJA), and for the 5th, 50th, and 95th percentiles. The ensemble median is represented by a solid black line, while individual EURO-CORDEX models appear as grey dashed lines. The model spread, calculated as the standard deviation across models, is shown as a grey shaded area. CERRA is depicted in orange. No lapse-rate correction is applied in this case, and data are grouped by the elevation of each model or reference dataset.#

📋 Methodology#

A subset of 39 models from EURO-CORDEX is compared to E-OBSv30.0e to assess the elevation dependency of temperature biases. Following the approach of [3], we evaluate differences between the RCMs and E-OBS in representing the 5th, 50th, and 95th percentiles of temperature at various altitude ranges, for both summer and winter, across the Greater Alpine Region (GAR; 4–19°E, 43–49°N, 0–3500 m a.s.l.; [5][6]). The extent of the GAR domain can be seen in Figure .2 - GAR reproduced from Haslinger et al., 2019 [5] under the CC BY 4.0.

To assess consistency across reference datasets, CERRA—a high-resolution (5.5 km) regional reanalysis produced using the HARMONIE-ALADIN limited-area numerical weather prediction and data assimilation system—is also compared to E-OBS and the RCMs.

All datasets are regridded to a 0.11° grid corresponding to a selected RCM (user-defined). There is no clear consensus in the literature on the optimal regridding approach: regridding to a finer resolution can be useful for certain applications but risks introducing artificial spatial detail not supported by the underlying data, whereas regridding to a coarser grid preserves the original physical consistency. In this work, we have chosen to regrid to the coarser resolution, following the approach in [7].

While regridding enables consistent spatial comparison, it does not inherently align the elevations of different datasets, which may still differ due to variations in underlying orography. To address this, a lapse-rate correction is applied to adjust all datasets to the same target elevation. CERRA’s elevation (regridded to 0.11°) is used as the target, as CERRA originally has the highest spatial resolution. A spatially and temporally uniform lapse rate of 0.0065 °C m⁻¹ is applied to all regridded datasets—including E-OBS and the RCMs—following a procedure similar to [7]. Differences in temperatures before and after this correction are evaluated to determine whether the adjustment produces substantial changes.

The analysis and results follow the next outline:

1. Parameters, requests and functions definition

1.1. Import packages
1.2. Define Parameters
1.3. Define models
1.4. Define CERRA request
1.5. Define E-OBS request
1.6. Define model requests
1.7. Functions to cache

2. Downloading and processing

2.1. Download and transform the regridding model
2.2. Download and transform CERRA
2.3. Download and transform E-OBS
2.4. Download and transform models
2.5. Apply land-sea mask

3. Plot and describe results

3.1. Define plotting functions
3.2.Elevation profiles of biases relative to E-OBS
3.3. Elevation profiles of biases after applying lapse-rate correction
3.4. Elevation profiles of the impact of lapse-rate correction
3.5. Results summary
3.6. Implications for the users

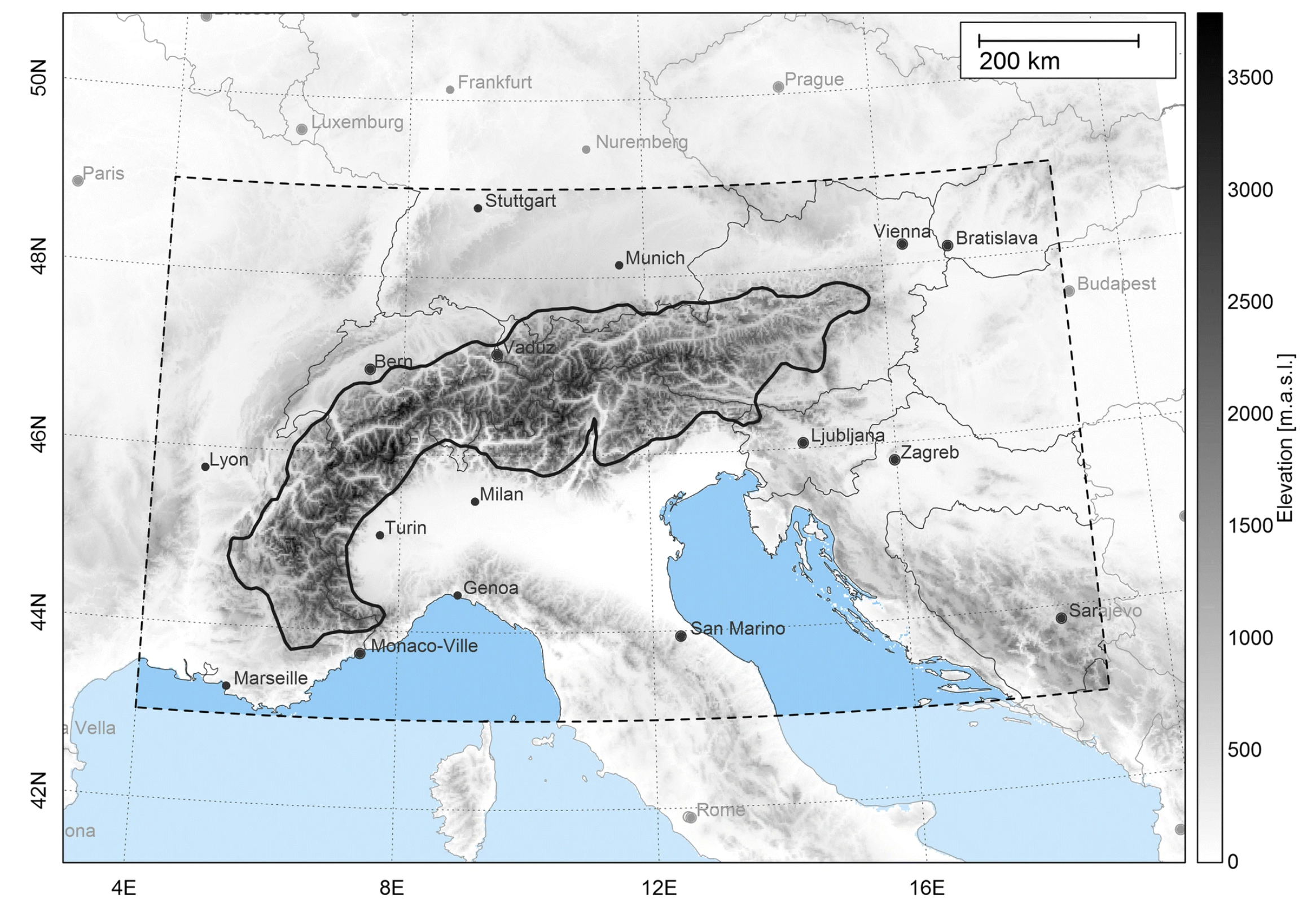
Fig. 5.2.6.2 Map of Central and Southern Europe. The broken line indicates the boundaries of the Greater Alpine Region; the solid line represents a generalized outline of the 1000 m a.s.l. isoline of the Alps which should help in locating the mountainous areas of the domain in the following figures. Image reproduced from *Figure 1* in Haslinger et al., 2019 [5], under the CC BY 4.0#

📈 Analysis and results#

1. Parameters, requests and functions definition#

1.1. Import packages#

1.2. Define Parameters#

In the “Define Parameters” section, various customisable options for the notebook are specified:

The start and end years of the historical period can be specified using the year_start and year_stop parameters. The default period, 1986–2005, is selected to maximise dataset availability while avoiding the need to include future projection data.
The chunk selection allows the user to define if dividing into chunks when downloading the data on their local machine. Although it does not significantly affect the analysis, it is recommended to keep the default value for optimal performance.
variable and collection_id are not customisable for this assessment and are set to ‘temperture’ and ‘CORDEX’. Expert users can use this notebook as a guide to create similar analyses for other variables or model sets.
area defines the geographical domain over which the analysis will be performed. Note that this notebook is designed for the EURO-CORDEX domain, so the selected area must lie within its boundaries. The Greater Alpine Region (GAR; 4–19°E, 43–49°N, 0–3500 m a.s.l.; [5][6]) is choosen for this assessment.
rcm_model_regrid and gcm_driven_model_regrid specify the EURO-CORDEX regional climate model and the driving global climate model, respectively, whose grid will be used as the target for remapping. Note that both models must be included in the matrix of RCM-GCM combinations defined by the models_cordex dictionary in Section 1.3.

1.3. Define models#

The following climate analyses are conducted using the EURO-CORDEX models available at the time of download, limited to those that include the orography variable in the Climate Data Store (CDS).

1.4. Define CERRA request#

Within this notebook, CERRA is also used to stress the sensitivity of results to the choice of reference dataset. In this section, we define the necessary parameters for the cds-api data request for CERRA.

1.5. Define E-OBS request#

Within this notebook, E-OBS serves as the reference product. In this section, we set the required parameters for the cds-api data-request of E-OBS.

1.6. Define model requests#

In this section we set the required parameters for the cds-api data-request of EURO-CORDEX models.

Show code cell source

Hide code cell source

models_r1i1p1_orog=["cnrm_aladin63","dmi_hirham5","mohc_hadrem3_ga7_05","knmi_racmo22e"] 
request_cordex = {
    "format": "zip",
    "domain": "europe",
    "experiment": "historical",
    "horizontal_resolution": "0_11_degree_x_0_11_degree",
    "temporal_resolution": "daily_mean",
    "variable": [cordex_variable],
    "ensemble_member": "r1i1p1",
}

def get_cordex_years(
    year_start,
    year_stop,
    start_years=list(range(1951, 2097, 5)),
    end_years=list(range(1955, 2101, 5)),
):
    start_year = []
    end_year = []
    years = set(range(year_start, year_stop + 1))
    for start, end in zip(start_years, end_years):
        if years & set(range(start, end + 1)):
            start_year.append(start)
            end_year.append(end)
    return start_year, end_year


model_requests = {}

for gcm_model in gcm_models:
    for model in models_cordex[gcm_model]:
        start_years = list(range(year_start, year_stop+1, 5))
        end_years = list(range(year_start+4, year_stop+5, 5))
        model_requests[f"{gcm_model}_{model}"] = (
            "projections-cordex-domains-single-levels",
            [
                {
                    "rcm_model": model,
                    "gcm_model": gcm_model,
                    **request_cordex,
                    "start_year": [str(start_year)],
                    "end_year": [str(end_year)],
                }
                for start_year, end_year in zip(
                    *get_cordex_years(
                        year_start,
                        year_stop,
                        start_years=start_years,
                        end_years=end_years,
                    )
                )
            ],
        )

request_grid_out = model_requests[model_regrid]

model_requests_orography = {}
for gcm_model in gcm_models:
    for model in models_cordex[gcm_model]:
        gcm_rcm_combination=f"{gcm_model}_{model}"
        model_requests_orography[gcm_rcm_combination]=(
            "projections-cordex-domains-single-levels",
            [
                {
                    "domain": "europe",
                    "experiment": "rcp_8_5" if gcm_rcm_combination in ["mpi_m_mpi_esm_lr_uhoh_wrf361h","ncc_noresm1_m_cnrm_aladin63"] else "historical",
                    "horizontal_resolution": "0_11_degree_x_0_11_degree",
                    "temporal_resolution": "fixed",
                    "variable": ["orography"],
                    "gcm_model": gcm_model,
                    "rcm_model": model,
                    "ensemble_member":"r1i1p1" if model in models_r1i1p1_orog else "r0i0p0",
                }
            ]
        )

request_orography_grid_out=model_requests_orography[model_regrid]

1.7. Functions to cache#

In this section, functions that will be executed in the caching phase are defined. Caching is the process of storing copies of files in a temporary storage location, so that they can be accessed more quickly. This process also checks if the user has already downloaded a file, avoiding redundant downloads.

Description of the main functions:

compute_percentiles: This function resamples data to daily frequency if needed (e.g., for hourly CERRA data), performs regridding to the target grid, selects the subregion of interest, and calculates the 5th, 50th, and 95th percentiles for summer and winter.
orog_regrid: This function regrids the orography data from the models, E-OBS and CERRA onto the selected RCM grid (defined by the model_regrid parameter), enabling a subsequent point-by-point lapse-rate correction.

Show code cell source

Hide code cell source

def select_timeseries(ds, timeseries="JJA", year_start=None, year_stop=None):
    if timeseries == "JJA":
        season_months = [6, 7, 8]
    elif timeseries == "DJF":
        season_months = [12, 1, 2]
    else:
        raise ValueError(f"Unsupported season: {timeseries}")

    # Ensure time is datetime type
    time = ds.indexes["time"]
    if not np.issubdtype(time.dtype, np.datetime64):
        ds["time"] = xr.decode_cf(ds).time

    # Filter by years
    ds = ds.sel(time=slice(f"{year_start}-01-01", f"{year_stop}-12-31"))

    # Filter by season
    ds_season = ds.where(ds["time.month"].isin(season_months), drop=True)
    return ds_season

def get_p(ds, percentile):
    return ds.quantile(percentile/100, dim="time", skipna=True)

def add_bounds(ds):
    for coord in {"latitude", "longitude"} - set(ds.cf.bounds):
        ds = ds.cf.add_bounds(coord)
    return ds

def get_grid_out(request_grid_out, method):
    ds_regrid = download.download_and_transform(*request_grid_out)
    coords = ["latitude", "longitude"]
    if method == "conservative":
        ds_regrid = add_bounds(ds_regrid)
        for coord in list(coords):
            coords.extend(ds_regrid.cf.bounds[coord])
    grid_out = ds_regrid[coords]
    coords_to_drop = set(grid_out.coords) - set(coords) - set(grid_out.dims)
    grid_out = ds_regrid[coords].reset_coords(coords_to_drop, drop=True)
    grid_out.attrs = {}
    return grid_out


def compute_percentiles(
    ds,
    year_start,
    year_stop,
    area,
    resample_reduction=None,
    request_grid_out=None,
    **regrid_kwargs,
):
    assert (request_grid_out and regrid_kwargs) or not (
        request_grid_out or regrid_kwargs
    )
    ds = ds.drop_vars([var for var, da in ds.data_vars.items() if len(da.dims) != 3])
    ds = ds[list(ds.data_vars)]
    ds=ds.convert_calendar('proleptic_gregorian', align_on='date', use_cftime=False)
    ds = ds.sel(time=slice(f"{year_start}-01-01", f"{year_stop}-12-31"))

    # Select a subdomain
    regionalise_kwargs = {
        "lon_slice": slice(area[1], area[3]),
        "lat_slice": slice(area[0], area[2]),
    }


    if resample_reduction:
        resampled = ds.resample(time="1D")
        ds = getattr(resampled, resample_reduction)(keep_attrs=True)

    # Original bounds for conservative interpolation
    if regrid_kwargs.get("method") == "conservative":
        ds = add_bounds(ds)
        bounds = [
            ds.cf.get_bounds(coord).reset_coords(drop=True)
            for coord in ("latitude", "longitude")
        ]
    else:
        bounds = []

    if request_grid_out:
        ds = diagnostics.regrid(
            ds.merge({da.name: da for da in bounds}),
            grid_out=get_grid_out(request_grid_out, regrid_kwargs["method"]),
            **regrid_kwargs,
        )
    ds = utils.regionalise(ds, **regionalise_kwargs)


    # Compute percentiles 
    data_dict = {}
    for season in ["jja", "djf"]:
        ds_season = select_timeseries(
            ds, timeseries=season.upper(), year_start=year_start, year_stop=year_stop
        ).chunk({"time": -1})
        for p in [5, 50, 95]:
            key = f"p{p}_{season}"
            data_dict[key] = list(get_p(ds_season, p).data_vars.values())[0]


    ds= xr.merge([xr.Dataset({k: v}) for k, v in data_dict.items()], compat="override")
    return ds

def orog_regrid(
    ds,
    area,
    request_grid_out=None,
    **regrid_kwargs,
):
    # Select a subdomain
    regionalise_kwargs = {
        "lon_slice": slice(area[1], area[3]),
        "lat_slice": slice(area[0], area[2]),
    }
    # Original bounds for conservative interpolation
    if regrid_kwargs.get("method") == "conservative":
        ds = add_bounds(ds)
        bounds = [
            ds.cf.get_bounds(coord).reset_coords(drop=True)
            for coord in ("latitude", "longitude")
        ]
    else:
        bounds = []
    if request_grid_out:  
        ds = diagnostics.regrid(
                ds.merge({da.name: da for da in bounds}),
                grid_out=get_grid_out(request_grid_out, regrid_kwargs["method"]),
                **regrid_kwargs,
            )
    ds = utils.regionalise(ds, **regionalise_kwargs)
    return ds

2. Downloading and processing#

2.1. Download and transform the regridding model#

In this section, the download.download_and_transform function from the c3s_eqc_automatic_quality_control package is employed to download daily data from the selected EURO-CORDEX regridding model, select the subregion of interest, and calculate the 5th, 50th, and 95th percentiles for summer and winter over the period 1986–2005, caching the results to avoid redundant downloads and processing.

The regridding model here refers to the model whose grid is used as the target grid for remapping the other models, as well as CERRA5 and E-OBS. This ensures all datasets share a common grid, facilitating direct comparison at each grid cell. Within this notebook, the regridding model is set to "ichec_ec_earth_smhi_rca4" but it can be changed by modifying the gcm_driven_model_regrid and rcm_model_regrid parameters in Section 1.2. Note that both models must be included in the matrix of RCM-GCM combinations defined by the models_cordex dictionary in Section 1.3. It is important to highlight that the choice of the target grid can impact the analysis depending on the specific application.

2.2. Download and transform CERRA#

In this section, the download.download_and_transform function from the c3s_eqc_automatic_quality_control package is used to download sub-daily data from CERRA, resample it to daily frequency, regrid to the target grid, select the subregion of interest, and compute the 5th, 50th, and 95th percentiles for summer and winter over the period 1986–2005. The results are cached to avoid redundant downloads and processing. Elevation data is also retrieved and regridded to the target grid (defined by the model_regrid parameter), as it is required to perform the lapse-rate correction.

2.3. Download and transform E-OBS#

In this section, the download.download_and_transform function from the c3s_eqc_automatic_quality_control package is used to download daily data from E-OBS, regrid to the target grid, select the subregion of interest, and compute the 5th, 50th, and 95th percentiles for summer and winter over the period 1986–2005. The results are cached to avoid redundant downloads and processing. Elevation data is also retrieved and regridded to the target grid (defined by the model_regrid parameter), as it is required to perform the lapse-rate correction.

2.4. Download and transform models#

In this section, the download.download_and_transform function from the c3s_eqc_automatic_quality_control package is used to download daily data from the selected EURO-CORDEX models, regrid to the target grid, select the subregion of interest, and compute the 5th, 50th, and 95th percentiles for summer and winter over the period 1986–2005. The results are cached to avoid redundant downloads and processing. Elevation data is also retrieved and regridded to the target grid (defined by the model_regrid parameter), as it is required to perform the lapse-rate correction.

model='cccma_canesm2_gerics_remo2015'
model='cnrm_cerfacs_cm5_clmcom_eth_cosmo_crclim'
model='cnrm_cerfacs_cm5_cnrm_aladin63'
model='cnrm_cerfacs_cm5_dmi_hirham5'
model='cnrm_cerfacs_cm5_gerics_remo2015'
model='cnrm_cerfacs_cm5_knmi_racmo22e'
model='cnrm_cerfacs_cm5_mohc_hadrem3_ga7_05'
model='ichec_ec_earth_clmcom_eth_cosmo_crclim'
model='ichec_ec_earth_dmi_hirham5'
model='ichec_ec_earth_knmi_racmo22e'
model='ichec_ec_earth_smhi_rca4'
model='ipsl_cm5a_mr_dmi_hirham5'
model='ipsl_cm5a_mr_gerics_remo2015'
model='ipsl_cm5a_mr_knmi_racmo22e'
model='ipsl_cm5a_mr_smhi_rca4'
model='miroc_miroc5_clmcom_clm_cclm4_8_17'
model='miroc_miroc5_gerics_remo2015'
model='mohc_hadgem2_es_clmcom_clm_cclm4_8_17'
model='mohc_hadgem2_es_cnrm_aladin63'
model='mohc_hadgem2_es_dmi_hirham5'
model='mohc_hadgem2_es_gerics_remo2015'
model='mohc_hadgem2_es_knmi_racmo22e'
model='mohc_hadgem2_es_mohc_hadrem3_ga7_05'
model='mohc_hadgem2_es_smhi_rca4'
model='mpi_m_mpi_esm_lr_clmcom_clm_cclm4_8_17'
model='mpi_m_mpi_esm_lr_clmcom_eth_cosmo_crclim'
model='mpi_m_mpi_esm_lr_cnrm_aladin63'
model='mpi_m_mpi_esm_lr_dmi_hirham5'
model='mpi_m_mpi_esm_lr_knmi_racmo22e'
model='mpi_m_mpi_esm_lr_mohc_hadrem3_ga7_05'
model='mpi_m_mpi_esm_lr_mpi_csc_remo2009'
model='mpi_m_mpi_esm_lr_smhi_rca4'
model='mpi_m_mpi_esm_lr_uhoh_wrf361h'
model='ncc_noresm1_m_cnrm_aladin63'
model='ncc_noresm1_m_dmi_hirham5'
model='ncc_noresm1_m_gerics_remo2015'
model='ncc_noresm1_m_knmi_racmo22e'
model='ncc_noresm1_m_mohc_hadrem3_ga7_05'
model='ncc_noresm1_m_smhi_rca4'

2.5. Apply land-sea mask#

This section applies a land–sea mask to all models, as well as to CERRA and E-OBS, to ensure consistency in the land-only analysis.

100%|██████████| 1/1 [00:00<00:00, 20.27it/s]

3. Plot and describe results#

This section will display the following results:

Elevation profiles of biases relative to E-OBS: Differences compared to the E-OBS vertical profile are shown for each EURO-CORDEX model individually, the ensemble median, the spread (calculated as the standard deviation), and CERRA. Profiles are plotted separately for winter (DJF) and summer (JJA), and for the 5th, 50th, and 95th percentiles.
Elevation profiles of biases after applying lapse-rate correction: As above, this includes each EURO-CORDEX model, the ensemble median, the spread, and CERRA, for both seasons and selected percentiles, but with all datasets corrected to CERRA’s elevation (regridded to 0.11°) using a uniform lapse rate.
Elevation profiles of the impact of lapse-rate correction: This shows the difference between the corrected and uncorrected profiles for E-OBS, individual EURO-CORDEX models, the ensemble median, and the spread.

3.1. Define plotting functions#

The functions compute_elevation_profile, plot_differences_vs_eobs, plot_lapse_rate_impact and apply_lapse_rate_correction are used to generate and visualise the elevation-dependent biases of temperature. Specifically:

compute_elevation_profile calculates the vertical (elevation-based) profiles of the 5th, 50th, and 95th percentiles for each dataset (EURO-CORDEX models, CERRA, and E-OBS), separately for winter (DJF) and summer (JJA).
apply_lapse_rate_correction adjusts temperatures to account for differences in elevation by applying a uniform lapse rate (−0.0065 °C m⁻¹), bringing the regridded models and E-OBS to the same elevation as CERRA (regridded to 0.11°).
plot_differences_vs_eobs plots the differences (biases) between the elevation profiles of the EURO-CORDEX models and CERRA, relative to that of E-OBS, for each percentile and season.
plot_lapse_rate_impact highlights the change introduced by the lapse-rate correction, showing the difference between corrected and uncorrected profiles for each dataset.

In the plots, the ensemble median is represented by a solid black line, while individual EURO-CORDEX models appear as grey dashed lines. The model spread, calculated as the standard deviation across models, is shown as a grey shaded area. CERRA is depicted in orange. Finally, E-OBS is shown in blue, but only in the plots that assess the impact of the lapse-rate correction.

Show code cell source

Hide code cell source

def compute_elevation_profile(da, ds_orog, elev_bins=np.arange(0, 3050, 200), kelvin_to_celsius=True,trend=False):
    if trend==False:
        if kelvin_to_celsius:
            da = da - 273.15
    else:
        factor = 3.15576e17 
        da=da*factor
    values = da.values.flatten()
    elev = ds_orog["orog"].values.flatten()
    valid = ~np.isnan(values) & ~np.isnan(elev)
    values = values[valid]
    elev = elev[valid]
    elev_labels = (elev_bins[:-1] + elev_bins[1:]) / 2
    df = pd.DataFrame({'value': values, 'elev': elev})
    df['elev_bin'] = pd.cut(df['elev'], bins=elev_bins, labels=elev_labels)

    return df.groupby('elev_bin')['value'].mean()


def plot_differences_vs_eobs(ds_models_interpolated, ds_cerra, ds_eobs, corrected=False,
                             ds_orog_models=None, ds_orog_cerra=None,
                             ds_orog_eobs=None,ds_orog_target=None):

    if ds_orog_target is not None:
        ds_orog_model = ds_orog_target
        ds_orog_cerra = ds_orog_target 
        ds_orog_eobs = ds_orog_target
        
    fig, axs = plt.subplots(2, 3, figsize=(15, 10), sharex=True, sharey=True)
    percentiles = ["p5", "p50", "p95"]
    seasons = ["djf", "jja"]

    model_names = ds_models_interpolated.model.values
    elev_bins = np.arange(0, 3050, 200)
    elev_labels = (elev_bins[:-1] + elev_bins[1:]) / 2

    for i, season in enumerate(seasons):
        for j, p in enumerate(percentiles):
            varname = f"{p}_{season}"
            ax = axs[i, j]

            # Compute E-OBS and CERRA profiles
            profile_eobs = compute_elevation_profile(ds_eobs[varname], ds_orog_eobs, kelvin_to_celsius=False)
            profile_cerra = compute_elevation_profile(ds_cerra[varname], ds_orog_cerra)

            # Store model differences
            model_diffs = []

            for model in model_names:
                da_model = ds_models_interpolated[varname].sel(model=model)
                if ds_orog_target is None:
                    ds_orog_model=ds_orog_models.sel(model=model)
                profile_model = compute_elevation_profile(da_model, ds_orog_model)
                diff_model = profile_model - profile_eobs
                model_diffs.append(diff_model)

                ax.plot(
                    diff_model.values,
                    diff_model.index.astype(float),
                    linestyle="--",
                    color="grey",
                    alpha=0.5,
                    linewidth=1
                )

            # Convert to DataFrame for ensemble stats
            df_models = pd.DataFrame(model_diffs, index=model_names)
            median_diff = df_models.median(axis=0)
            std_diff = df_models.std(axis=0)


            # Plot ensemble median
            ax.plot(
                median_diff.values,
                median_diff.index.astype(float),
                color="black",
                label="Model ensemble median",
                linewidth=2
            )
            # Plot ensemble spread
            ax.fill_betweenx(
                median_diff.index.astype(float),
                (median_diff - std_diff).values,
                (median_diff + std_diff).values,
                color="lightgrey",
                alpha=0.5,
                label="Model ±1σ" if i == 0 and j == 0 else None
            )


            # Plot CERRA 
            diff_cerra = profile_cerra - profile_eobs
            ax.plot(
                diff_cerra.values,
                diff_cerra.index.astype(float),
                color="tab:orange",
                label="CERRA",
                linewidth=2
            )

            # Formatting
            ax.axvline(0, color="k", linestyle="--", linewidth=0.8)
            ax.set_title(f"{p.upper()} - {season.upper()}")
            if j == 0:
                ax.set_ylabel("Elevation (m)")
            if i == 1:
                ax.set_xlabel("Difference (°C)")
            # Add gridlines
            ax.grid(True, which='both', linestyle='--', alpha=0.5)

    # Shared legend
    handles, labels = axs[0, 0].get_legend_handles_labels()
    fig.legend(handles, labels, loc="lower center", ncol=3)
    plt.tight_layout(rect=[0, 0.05, 1, 1])
    plt.show()

def apply_lapse_rate_correction(ds, ds_orog_native, ds_orog_target, lapse_rate=-0.0065, varnames=None):
    corrected = ds.copy()
    if varnames is None:
        varnames = list(ds.data_vars)

    delta_z = ds_orog_target["orog"] - ds_orog_native["orog"]

    for var in varnames:
        corrected[var] = ds[var] + lapse_rate * delta_z

    return corrected

def plot_lapse_rate_impact(ds_models_interpolated, ds_eobs,
                                  ds_models_interpolated_corr,
                                  ds_eobs_corr, ds_orog, varname="p5_jja"):
    fig, ax = plt.subplots(figsize=(7, 8))

    model_names = ds_models_interpolated.model.values

    # --- Compute difference: corrected - original ---
    # E-OBS
    profile_eobs_before = compute_elevation_profile(ds_eobs[varname], ds_orog, kelvin_to_celsius=False)
    profile_eobs_after = compute_elevation_profile(ds_eobs_corr[varname], ds_orog, kelvin_to_celsius=False)
    diff_eobs = profile_eobs_after - profile_eobs_before

    # Models
    model_diffs = []
    for model in model_names:
        profile_model_before = compute_elevation_profile(
            ds_models_interpolated[varname].sel(model=model), ds_orog
        )
        profile_model_after = compute_elevation_profile(
            ds_models_interpolated_corr[varname].sel(model=model), ds_orog
        )
        diff_model = profile_model_after - profile_model_before
        model_diffs.append(diff_model)

        # Plot individual model differences
        ax.plot(
            diff_model.values,
            diff_model.index.astype(float),
            linestyle="--",
            color="grey",
            alpha=0.3,
            linewidth=1
        )

    # Ensemble statistics
    df_models = pd.DataFrame(model_diffs, index=model_names)
    median_diff = df_models.median(axis=0)
    std_diff = df_models.std(axis=0)

    # Plot ensemble median + spread
    ax.plot(
        median_diff.values,
        median_diff.index.astype(float),
        color="black",
        linewidth=2,
        label="Model ensemble median"
    )
    ax.fill_betweenx(
        median_diff.index.astype(float),
        (median_diff - std_diff).values,
        (median_diff + std_diff).values,
        color="lightgrey",
        alpha=0.5,
        label="Model ±1σ"
    )

    # Plot E-OBS
    ax.plot(
        diff_eobs.values,
        diff_eobs.index.astype(float),
        color="tab:blue",
        linewidth=2,
        label="E-OBS"
    )

    # Formatting
    ax.axvline(0, color="k", linestyle="--", linewidth=0.8)
    ax.set_ylabel("Elevation (m)")
    ax.set_xlabel("ΔT (°C, lapse rate corrected − uncorrected)")
    ax.grid(True, which='both', linestyle='--', alpha=0.5)
    ax.set_title("Impact of lapse-rate correction on temperature profiles")

    ax.legend(loc="best")
    plt.tight_layout()
    plt.show()

3.2.Elevation profiles of biases relative to E-OBS#

Differences compared to the E-OBS vertical profile are shown for each EURO-CORDEX model individually, the ensemble median, the spread (calculated as the standard deviation), and CERRA. Profiles are plotted separately for winter (DJF) and summer (JJA), and for the 5th, 50th, and 95th percentiles.

Note that no lapse-rate correction is applied in this case, and data are grouped by the elevation of each model or reference dataset.

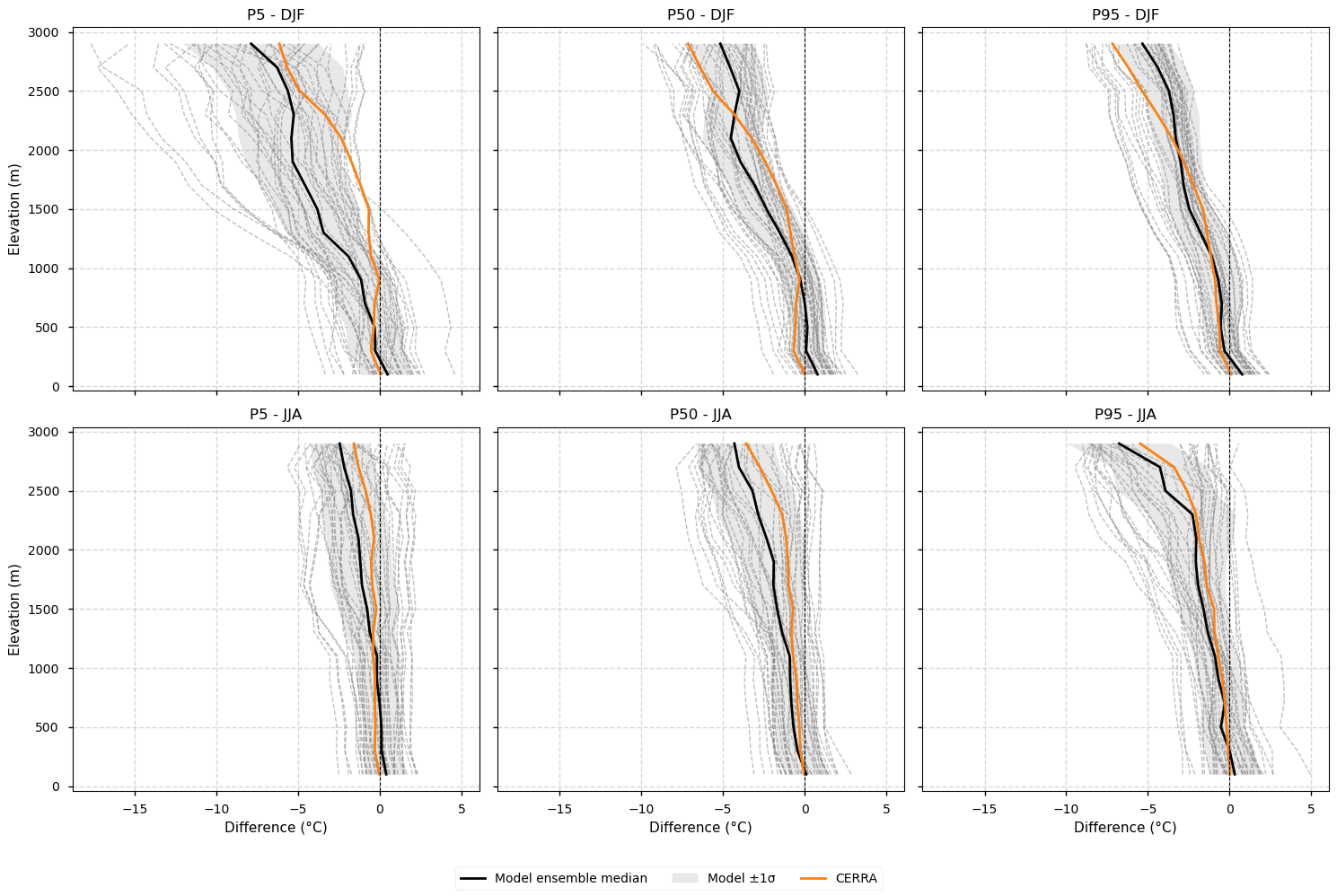
../../_images/efbd6f912b7e42058eaf6901523e2410b2eb13e794b0c3ecb1949483751f7998.png

Fig 3. Elevation profiles of biases relative to E-OBS. Differences compared to the E-OBS vertical profile are shown for each EURO-CORDEX model individually, the ensemble median, the spread (calculated as the standard deviation), and CERRA. Profiles are plotted separately for winter (DJF) and summer (JJA), and for the 5th, 50th, and 95th percentiles. The ensemble median is represented by a solid black line, while individual EURO-CORDEX models appear as grey dashed lines. The model spread, calculated as the standard deviation across models, is shown as a grey shaded area. CERRA is depicted in orange. No lapse-rate correction is applied in this case, and data are grouped by the elevation of each model or reference dataset.

3.3. Elevation profiles of biases after applying lapse-rate correction#

Differences compared to the E-OBS vertical profile are shown for each EURO-CORDEX model individually, the ensemble median, the spread (calculated as the standard deviation), and CERRA. Profiles are plotted separately for winter (DJF) and summer (JJA), and for the 5th, 50th, and 95th percentiles.

Note that in this case, each dataset is adjusted to a common target elevation—the CERRA orography regridded to 0.11°—using a uniform lapse-rate correction (−0.0065 °C m⁻¹) before computing the differences. For example, if a grid point in a model is 200 m lower than the corresponding point in the target CERRA, the temperature at that point is corrected by 200 m × −0.0065 °C m⁻¹ = −1.3 °C.

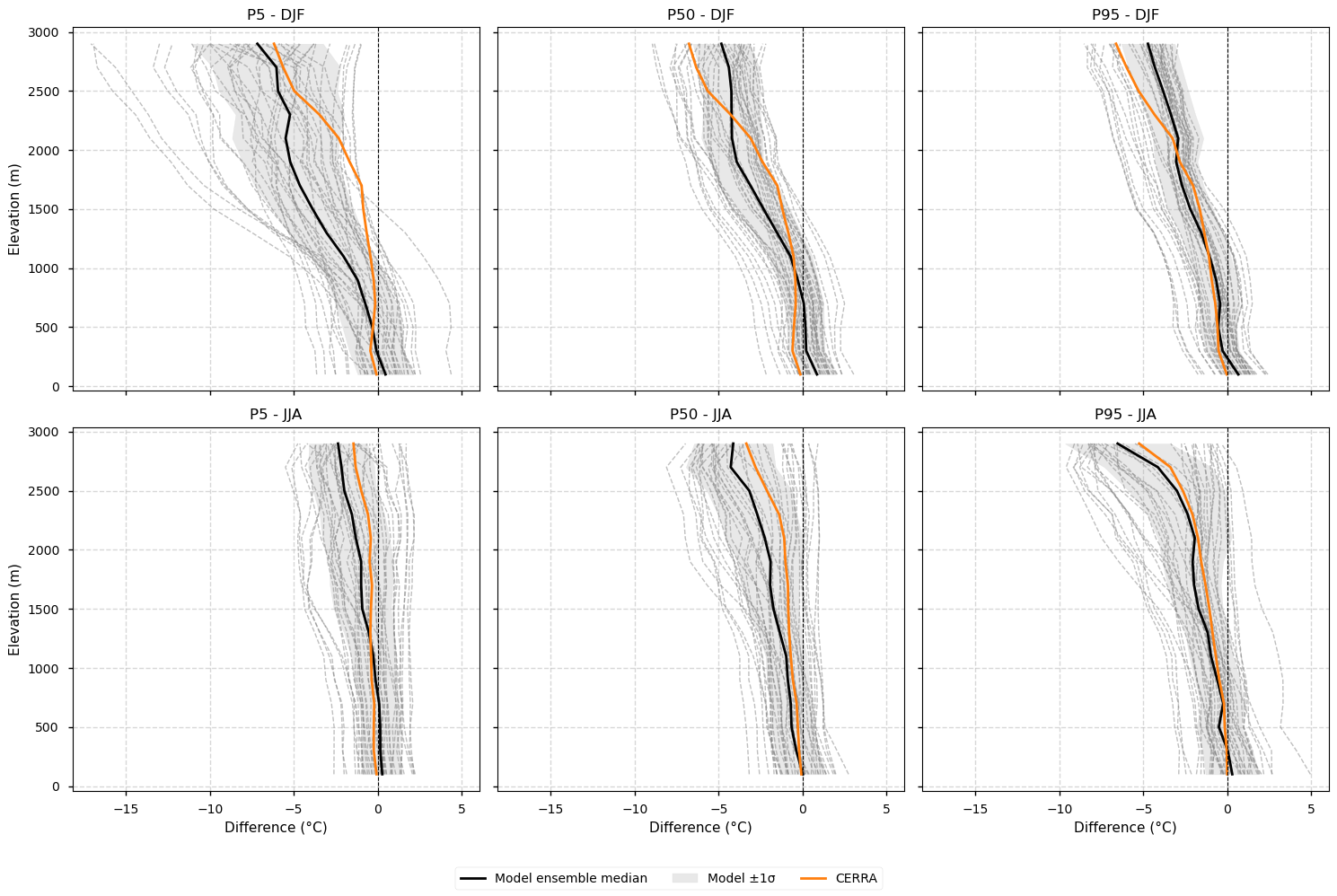
../../_images/4e3605c59f76aec2bc3813e68e9ba1abb50573ea450eb57ca0a7afcc8e54ff34.png

Fig 4. Elevation profiles of biases after applying lapse-rate correction. Differences compared to the E-OBS vertical profile are shown for each EURO-CORDEX model individually, the ensemble median, the spread (calculated as the standard deviation), and CERRA. Profiles are plotted separately for winter (DJF) and summer (JJA), and for the 5th, 50th, and 95th percentiles. The ensemble median is represented by a solid black line, while individual EURO-CORDEX models appear as grey dashed lines. The model spread, calculated as the standard deviation across models, is shown as a grey shaded area. CERRA is depicted in orange. Each dataset is adjusted to a common target elevation—the CERRA orography regridded to 0.11°—using a uniform lapse-rate correction (−0.0065 °C m⁻¹) before computing the differences. For example, if a grid point in a model is 200 m lower than the corresponding point in the target CERRA, the temperature at that point is corrected by 200 m × −0.0065 °C m⁻¹ = −1.3 °C.

3.4. Elevation profiles of the impact of lapse-rate correction#

This section highlights the change introduced by the lapse-rate correction. The temperature at each grid point of every model has been previously adjusted using a uniform lapse rate of −0.0065 °C m⁻¹ to align all datasets to the same target elevation, defined by the regridded CERRA orography (0.11° resolution). For example, if a grid point in a model is 200 m lower than the corresponding point in the target CERRA, the temperature at that point is corrected by 200 m × −0.0065 °C m⁻¹ = −1.3 °C. The plot below shows the vertical profiles of these differences, illustrating how the lapse-rate correction affects temperatures across elevation bands. In other words, it shows the difference between assuming that all models and reference datasets share the same elevation after regridding (as sometimes assumed in the literature) and applying a correction to account for residual elevation differences.

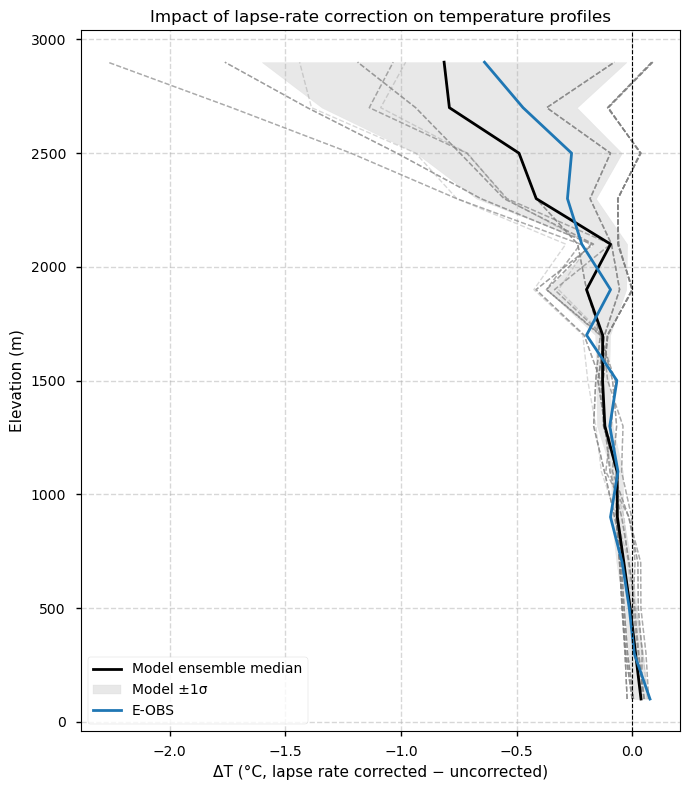
../../_images/437deb70ae23366ad92c7cd13632fe85d7e6b1a7541f66bb9ef22a461f265536.png

Fig 5. Elevation profiles of the impact of lapse-rate correction. The plot shows differences between lapse-rate corrected and uncorrected temperature profiles for E-OBS and EURO-CORDEX models. The correction adjusts temperatures to a common target elevation (that of regridded CERRA at 0.11°) using a uniform lapse rate (−0.0065 °C m⁻¹), ensuring consistent comparison across datasets. Negative values indicate that regridded model or E-OBS elevations are lower than CERRA. E-OBS is shown as a solid blue line, the ensemble median as a solid black line, individual models as grey dashed lines and the inter-model spread (standard deviation) as a grey shaded area. CERRA is not displayed since it defines the elevation target.

3.5. Results summary#

Regional Climate Models (RCMs) show biases relative to both reference datasets (E-OBS and CERRA).
Systematic cold biases are observed in RCMs above 1000–1500 m during winter across the 5th, 50th, and 95th percentiles when evaluated against E-OBS, consistent with findings from [3].
CORDEX biases relative to CERRA are smaller in magnitude and do not increase systematically with altitude, unlike the case with E-OBS.
Biases relative to E-OBS generally increase with elevation (becoming more negative), particularly for the 5th percentile in winter, where the ensemble median reaches its largest negative value.
Even in summer, models exhibit negative biases at higher elevations relative to E-OBS, notably for the 50th and 95th percentiles.
The greatest inter-model spread occurs for the 5th percentile in winter.
CERRA shows large cold differences relative to E-OBS; for the 50th and 95th percentiles in winter, it is colder than the CORDEX ensemble median above 2000–2500 m.
Applying a lapse-rate correction to ensure all datasets are compared at the same elevation does not substantially alter the shape of the vertical bias profiles.
The lapse-rate correction introduces small (generally <1 °C) negative differences that increase with elevation, reflecting that regridded model and E-OBS elevations are typically lower than those of regridded CERRA.

3.6. Implications for the users#

Elevation-dependent biases in RCM outputs are systematic and significant above 1000–1500 m, particularly in winter, when evaluated against E-OBS, and affect all percentiles. Users working with climate data in mountainous regions should be aware that cold biases tend to intensify with elevation, especially for cold extremes (5th percentile), potentially influencing impact assessments and adaptation planning.
Bias magnitude and inter-model spread vary by season and percentile, with the greatest variability observed in winter cold tails (5th percentile). This highlights substantial uncertainty for extreme cold conditions at high elevations, which should be explicitly considered in risk and vulnerability evaluations.
CERRA exhibits strong cold differences when compared to E-OBS. This has two key implications: (1) caution is needed when using CERRA as a reference or input dataset for mountain climate analyses, and (2) despite its high resolution, the underlying model may not adequately represent complex high-altitude dynamics and processes.
A critical caveat lies in the inherent uncertainty and sparsity of observational data at high elevations, particularly in E-OBS. These limitations—stemming from sparse station coverage, complex topography, and measurement challenges—can cause some of the apparent model biases to actually reflect deficiencies in the reference data.
Interpolation accuracy generally declines with reduced station density, performs worse for spatially variable parameters (e.g. precipitation), and deteriorates further in areas of complex terrain such as mountainous regions [8]. Moreover, in some cases, E-OBS tends to report warmer values than national station datasets across the 5th, 50th, and 95th percentiles [3], and has been shown to overestimate temperatures in the distribution tails, even over moderately complex orography [9].
Lapse-rate correction may slightly reduce biases by adjusting for elevation differences between datasets but does not fundamentally change the shape of vertical bias profiles. While useful for harmonising datasets, it is not a solution to the underlying model or observational issues driving the biases.
Where feasible, users may benefit from complementing gridded analyses with station-based evaluations corrected for elevation. While the CDS does not currently provide access to raw station-level data, external sources may be used.
Altogether, the combination of systematic model biases, observational uncertainties, and limited high-elevation data availability underscores the need for caution when interpreting temperature extremes and climate signals in mountainous regions.
Bias-adjustment methods do not ensure that corrected future projections will more accurately reflect reality, as the underlying biases may change under evolving climate conditions [10].

ℹ️ If you want to know more#

Key resources#

Some key resources and further reading were linked throughout this assessment.

Regional climate models - CORDEX: https://cds.climate.copernicus.eu/datasets/projections-cordex-domains-single-levels?tab=overview
Gridded observation dataset for Europe, E-OBS: https://cds.climate.copernicus.eu/datasets/insitu-gridded-observations-europe?tab=overview
CERRA sub-daily regional reanalysis data for Europe on single levels from 1984 to present: https://cds.climate.copernicus.eu/datasets/reanalysis-cerra-single-levels?tab=overview
High-resolution global climate models: https://highresmip.org/
Mountain tourism meteorological and snow indicators for Europe from 1950 to 2100 derived from reanalysis and climate projections: https://cds.climate.copernicus.eu/datasets/sis-tourism-snow-indicators?tab=overview

Code libraries used:

C3S EQC custom functions, c3s_eqc_automatic_quality_control, prepared by B-Open

References#

[1] Immerzeel, W.W., Lutz, A.F., Andrade, M. et al., 2020. Importance and vulnerability of the world’s water towers. Nature 577, 364–369. https://doi.org/10.1038/s41586-019-1822-y

[2] Rudisill, W., Rhoades, A., Xu, Z., and Feldman, D. R.,2024. Are Atmospheric Models Too Cold in the Mountains? The State of Science and Insights from the SAIL Field Campaign. Bull. Amer. Meteor. Soc., 105, E1237–E1264, https://doi.org/10.1175/BAMS-D-23-0082.1

[3] Matiu, M., Napoli, A., Kotlarski, S. et al., 2024. Elevation-dependent biases of raw and bias-adjusted EURO-CORDEX regional climate models in the European Alps. Clim Dyn 62, 9013–9030. https://doi.org/10.1007/s00382-024-07376-y

[4] Shrestha, S., Zaramella, M., Callegari, M., Greifeneder, F., Borga, M., 2023. Scale Dependence of Errors in Snow Water Equivalent Simulations Using ERA5 Reanalysis over Alpine Basins. Climate, 11, 154. https://doi.org/10.3390/cli11070154

[5] Haslinger, K., Holawe, F., and Blöschl, G., 2019. Spatial characteristics of precipitation shortfalls in the Greater Alpine Region—a data-based analysis from observations. Theor Appl Climatol 136, 717–731. https://doi.org/10.1007/s00704-018-2506-5

[6] Auer, I., Böhm, R., Jurkovic, A., Lipa, W., Orlik, A., Potzmann, R., Schöner, W., Ungersböck, M., Matulla, C., Briffa, K., Jones, P., Efthymiadis, D., Brunetti, M., Nanni, T., Maugeri, M., Mercalli, L., Mestre, O., Moisselin, J.-M., Begert, M., Müller-Westermeier, G., Kveton, V., Bochnicek, O., Stastny, P., Lapin, M., Szalai, S., Szentimrey, T., Cegnar, T., Dolinar, M., Gajic-Capka, M., Zaninovic, K., Majstorovic, Z. and Nieplova, E., 2007. HISTALP—historical instrumental climatological surface time series of the Greater Alpine Region. Int. J. Climatol., 27: 17-46. https://doi.org/10.1002/joc.1377

[7] Kotlarski, S., Szabó, P., Herrera S., et al., 2019. Observational uncertainty and regional climate model evaluation: A pan-European perspective. Int J Climatol. 39: 3730–3749. https://doi.org/10.1002/joc.5249

[8] Hofstra, N., Haylock, M., New, M., and Jones, P. D., 2009. Testing E-OBS European high-resolution gridded data set of daily precipitation and surface temperature, J. Geophys. Res., 114, D21101. https://doi.org/10.1029/2009JD011799

[9] Kyselý, J., and Plavcová, E., 2010. A critical remark on the applicability of E-OBS European gridded temperature data set for validating control climate simulations, J. Geophys. Res., 115, D23118. https://doi.org/10.1029/2010JD014123

[10] Schmith, T., Thejll, P., Berg, P., Boberg, F., Christensen, O. B., Christiansen, B., Christensen, J. H., Madsen, M. S., and Steger, C., 2021. Identifying robust bias adjustment methods for European extreme precipitation in a multi-model pseudo-reality setting, Hydrol. Earth Syst. Sci., 25, 273–290, https://doi.org/10.5194/hess-25-273-2021

CORDEX temperature biases over the Alpine region — assessment using E-OBS and CERRA

Contents

5.2.6. CORDEX temperature biases over the Alpine region — assessment using E-OBS and CERRA#

🌍 Use case: Investigating climate biases in mountain regions to inform the ski and hydrological sectors.#

❓ Quality assessment question#

📢 Quality assessment statement#

📋 Methodology#

📈 Analysis and results#

1. Parameters, requests and functions definition#

1.1. Import packages#

1.2. Define Parameters#

1.3. Define models#

1.4. Define CERRA request#

1.5. Define E-OBS request#

1.6. Define model requests#

1.7. Functions to cache#

2. Downloading and processing#

2.1. Download and transform the regridding model#

2.2. Download and transform CERRA#

2.3. Download and transform E-OBS#

2.4. Download and transform models#

2.5. Apply land-sea mask#

3. Plot and describe results#

3.1. Define plotting functions#

3.2.Elevation profiles of biases relative to E-OBS#

3.3. Elevation profiles of biases after applying lapse-rate correction#

3.4. Elevation profiles of the impact of lapse-rate correction#

3.5. Results summary#

3.6. Implications for the users#

ℹ️ If you want to know more#

Key resources#

References#