Gravimetric mass changes from satellite data: assessment of resolution and uncertainty of Greenland ice sheet mass changes for glaciological applications

logo

1.3.5. Gravimetric mass changes from satellite data: assessment of resolution and uncertainty of Greenland ice sheet mass changes for glaciological applications#

Production date: 31-05-2025

Dataset version: 4.0

Produced by: Yoni Verhaegen and Philippe Huybrechts (Vrije Universiteit Brussel)

🌍 Use case: Monitoring Greenland ice sheet mass changes in the 21st century for usage in the context of Earth System modelling#

❓ Quality assessment question#

  • “Is the C3S Greenland ice sheet mass balance dataset sufficiently adequate in terms of its spatio-temporal resolution and uncertainty to be used in glaciological modeling efforts?”

Ice sheets are significant contributors to current (and future) global sea-level rise, indicators of climatic changes, and key players regarding feedback mechanisms within the atmosphere, ocean, and cryosphere. Assessing ice sheet mass changes is essential for understanding these mechanisms. At present-day, the gravimetric method from satellite-based remote sensing offers one out of the three feasible ways to regularly and accurately monitor mass changes of the entire ice sheets at a regular basis (the others being the altimetric and input-output method). The “Gravimetric mass balance data for the Antarctic and Greenland ice sheets from 2003 to 2022 derived from satellite observations” dataset on the Climate Data Store (CDS) therefore provides valuable insights into the ice sheet’s mass changes. The dataset uses satellite gravimetry from the GRACE and GRACE-FO missions to detect changes in the Earth’s gravitational field. These are then translated into cumulative mass anomalies of ice above buoyancy for the grounded ice of both the Greenland (GrIS) and Antarctic (AIS) ice sheets [1, 2]. This notebook evaluates the dataset’s maturity for monitoring Greenland ice mass changes in the 21st century. More specifically, we will check whether the data are sufficiently adequate in terms of its spatio-temporal resolution and uncertainty to be applicable in glaciological modeling applications. For that, we use the dataset version 4.0.

📢 Quality assessment statements#

These are the key outcomes of this assessment

  • Mass change detection by GRACE(-FO) is a useful tool to quantify the total ice mass change of the GrIS (and AIS), and is one of the three main data acquisition methods that can extract ice mass change data from large spatial scales, such as the complete ice sheets, at a regular basis. GRACE(-FO) directly captures all relevant processes for ice mass change (from both mass balance and ice dynamics), but it also has its limitations of which the user should take note before using the product. A large problem with the C3S dataset is that no gridded mass change and error products are included for the ice sheets, as well as the presence of (occasionally very) high error/uncertainty values, primarily due to the large data acquisition footprint and corrections needed for mass redistribution in the atmosphere, ocean, soil and solid earth. Data gaps are also present (e.g. during the transition period between GRACE and GRACE-FO in 2017-2018 CE). These are not filled up or flagged, users need to identify them themselves.

  • Concerning the specific use case and user question, the C3S GRACE(-FO) data are found to be inadequate to be used in most “traditional” glaciological modeling efforts because it is (1) only a spatially aggregated time series and has no gridded data, (2) does not include a surface mass balance component separately (which is, for example, needed in the prognostic continuity equation for ice thickness changes), and (3) has (very) high uncertainty in certain months. The GRACE(-FO) data can, on the other hand, be used for other purposes. The data are particularly well-suited for the direct calculation and monitoring of ice sheet mass changes and sea level contribution, and/or the validation of mass change estimates from other independent methods (e.g. the input-output method or the validation of the temporal variability of a surface mass balance model from a regional climate model).

📋 Methodology#

Dataset description#

The total mass balance of an ice sheet is the difference between mass gained (mainly from snow accumulation) and mass lost (by ablation or solid ice discharge across the grounding line), which is the same as the net mass change of the ice sheet. Remote sensing techniques, such as the use of satellites, are an important feature to derive and study the mass changes of the ice sheets. The ice sheet mass change dataset provides monthly gravimetric mass balance (GMB) values and their uncertainty for the Greenland (GrIS) and also the Antarctic ice sheet (AIS). The data represent a time series of the cumulative mass changes (mass anomalies) of the ice above buoyancy of the ice sheets and their basins (including ice caps and glaciers) that are derived using satellite gravimetry data from the GRACE(-FO) missions. Data are available as time series for the whole ice sheet, as well as at the basin level, but no gridded data are provided. Data are available since 2002 with units in Gt (Gigatonnes). For a more detailed description of the data acquisition and processing methods, we refer to the documentation on the CDS and the ECMWF Confluence Wiki (Copernicus Knowledge Base).

The mass changes and their errors derived from GRACE(-FO) are expressed in Gt (Gigatonnes). It can also be translated into a volume, for example one Gt of water (density 1000 kg/m\(^3\)) is exactly one km\(^3\), while one Gt of ice (density 917 kg/m\(^3\)) in volume becomes 1.091 km\(^3\) of ice. GRACE(-FO) data are in fact considered to be the sum of mass changes driven by changing rates of solid ice discharge (i.e. the flux across the grounding line \(D\)) and mass changes driven by changing rates of ablation and accumulation (mainly the surface mass balance or \(SMB\)). What GRACE(-FO) actually detects are patterns of mass redistribution, indicating that a material should be redistributed (e.g. by ice dynamics or liquid discharge) in order for GRACE(-FO) to be able to detect gravity anomalies and the corresponding mass changes over certain locations. In that sense, an amount of melted ice being replaced by its mass-equivalent amount of meltwater at the same location would result in zero mass change.

The main advantage of GRACE(-FO) is that all processes directly contributing to ice sheet mass fluctuations are observed directly. Unlike the input-output method, SMB is therefore not involved explicitely in processing and it is not separated from ice flow dynamics. Moreover, gaps in the time series do not affect linear trend estimation as mass changes occurring during these gaps are still included in the subsequent solution. The main drawbacks of this technique are the large footprint of data acquisition and the fact that corrections must be made for mass redistribution in the atmosphere, ocean, soil and solid earth (e.g. glacial isostatic adjustment) in order to isolate mass changes relevant for the ice sheets.

Structure and (sub)sections#

1. Data preparation and processing

2. Quantifying Greenland Ice Sheet mass changes and their errors in space and time

3. Short summary and take-home messages

📈 Analysis and results#

1. Data preparation and processing#

1.1 Import packages#

First we load the packages:

Hide code cell source

 
import fsspec
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import matplotlib.ticker as mticker
import numpy as np
import xarray as xr
from scipy.stats import linregress
from matplotlib.gridspec import GridSpec
import re
from math import ceil
import pandas as pd
import calendar
import os
from c3s_eqc_automatic_quality_control import download
plt.style.use("seaborn-v0_8-notebook")

1.2 Define request and download#

Then we define the parameters, i.e. for which ice sheet (or which basins of these ice sheets) we want the mass change data to be extracted:

Hide code cell source

 
variables = ["GrIS_total", "GrIS_1", "GrIS_2", "GrIS_3", "GrIS_4", "GrIS_5", "GrIS_6", "GrIS_7", "GrIS_8"]

Then we define requests for download from the CDS and download and transform the glacier mass change data.

Hide code cell source

 
collection_id = "satellite-ice-sheet-mass-balance"
request = {
    "variable": "all",
    "format": "zip",
}
ds = download.download_and_transform(collection_id, request)
ds_err = ds[[f"{var}_er" for var in variables]].compute()
ds = ds[variables].compute()
ds = xr.combine_by_coords([ds, ds_err])
print("Downloading done.")

100%|██████████| 1/1 [00:04<00:00,  4.46s/it]
                                             

Downloading done.

1.3 Display and inspect data#

Let us inspect the data:

Hide code cell source

 
ds

<xarray.Dataset> Size: 17kB
Dimensions:        (time: 216)
Coordinates:
  * time           (time) datetime64[ns] 2kB 2002-04-16T20:23:54.375000 ... 2...
Data variables: (12/18)
    GrIS_total     (time) float32 864B 1.057e+03 1.123e+03 ... -3.762e+03
    GrIS_1         (time) float32 864B 54.15 42.37 52.4 ... -440.0 -471.2 -441.5
    GrIS_2         (time) float32 864B 97.2 125.0 43.44 ... 28.75 80.42 17.64
    GrIS_3         (time) float32 864B 219.8 216.2 132.5 ... -467.5 -533.6
    GrIS_4         (time) float32 864B 140.1 152.3 129.0 ... -548.1 -498.9
    GrIS_5         (time) float32 864B 76.06 68.17 53.5 ... -288.9 -316.6 -274.7
    ...             ...
    GrIS_3_er      (time) float32 864B 45.75 25.68 20.46 ... 16.83 18.87 19.34
    GrIS_4_er      (time) float32 864B 42.49 30.83 25.91 ... 18.51 18.26 22.87
    GrIS_5_er      (time) float32 864B 26.84 32.99 18.78 ... 12.84 11.66 11.76
    GrIS_6_er      (time) float32 864B 73.16 41.97 28.93 ... 22.61 24.26 25.49
    GrIS_7_er      (time) float32 864B 57.64 41.52 19.34 ... 23.11 25.23 26.11
    GrIS_8_er      (time) float32 864B 59.26 63.21 45.86 ... 22.68 22.85 21.76
Attributes:
    Title:                GMB for Greenland and Antarctica ice sheets from th...
    institution:          DTU Space - Geodesy and Earth Observations
    reference:            Baratta et al. (2016), Groh and Horwart (2016)
    file_creation_date:   Tue May 16 09:49:32 2023
    region:               Greenland and Antarctica
    missions_used:        GRACE and and GRACE-FO
    time_coverage_start:  Apr-2002
    time_coverage_end:    Dec-2022
    Tracking_id:          ab2360a4-82d5-42f3-babb-90ce976a8a8e
    netCDF_version:       NETCDF4
    product_version:      4.0
    Summary:              This data set is prepared for the C3S project, and ...

It is a dataset that consists of several time series data, containing cumulative values of the total ice sheet mass change (cumulative mass anomalies) of, in this notebook, the entire Greenland Ice Sheet (GrIS_total) or its basins (GrIS_{basin_number}), as well as their uncertainty (GrIS_total_er and GrIS_{basin_number}_er) since 2002. For basin definitions and delineation, see Zwally et al. (2012) [3]. Mass changes and their uncertainty are expressed in units of Gt and the time period between two measurements is variable but mostly at monthly-spaced intervals. Note that no gridded data are given in this dataset, and hence no spatial resolution can be derived.

1.4 Data handling and creating functions#

Let us perform some data handling before getting started with the analysis:

Hide code cell source

 
variables_to_drop = [var for var in ds.data_vars if '_er' in var]
ds = ds.drop_vars(variables_to_drop)

year_to_ns = 1.0e9 * 60 * 60 * 24 * 365
with xr.set_options(keep_attrs=True):
    ds = ds - ds.isel(time=0)
for var, da in ds.data_vars.items():
    da.attrs["region"] = da.attrs["long_name"].split("_", 1)[0].title()
    da.attrs["long_name"] = "Cumulative mass change"
for var_name, da in ds.data_vars.items():
    # Check if the variable name contains a number
    match = re.search(r'_(\d+)', var_name)
    if match:
        basin_number = match.group(1)
        da.attrs["region"] = f"Greenland basin {basin_number}"
    else:
        da.attrs["region"] = f"Cumulative mass change of the Greenland Ice Sheet from GRACE(-FO)"

for var, da in ds_err.data_vars.items():
    da.attrs["region"] = da.attrs["long_name"].split("_", 1)[0].title()
    da.attrs["long_name"] = "Mass change error"
for var_name, da in ds_err.data_vars.items():
    # Check if the variable name contains a number
    match = re.search(r'_(\d+)', var_name)
    if match:
        basin_number = match.group(1)
        da.attrs["region"] = f"Greenland basin {basin_number}"
    else:
        da.attrs["region"] = f"Mass change error of the Greenland Ice Sheet from GRACE(-FO)"

with xr.set_options(keep_attrs=True):
    ds_diff = ds.diff("time") / ds["time"].diff("time").astype(int)
    ds_diff *= year_to_ns / 12
for var_name, da in ds_diff.data_vars.items():
    # Check if the variable name contains a number
    match = re.search(r'_(\d+)', var_name)
    if match:
        basin_number = match.group(1)
        da.attrs["region"] = f"Greenland basin {basin_number}"
    else:
        da.attrs["region"] = f"Non-cumulative mass change of the Greenland Ice Sheet from GRACE(-FO)"
    da.attrs["long_name"] = "Mass change"

We also define a plotting function to visualize the time series:

Hide code cell source

 
def plot_timeseries(ds, dataset_type="default"):
    variables = list(ds.data_vars.values())
    num_vars = len(variables)
    
    # Create a GridSpec layout with enough rows
    num_rows = (num_vars + 1) // 2  # Integer division, ensuring enough rows
    
    fig = plt.figure(figsize=(8, 3 * num_rows))
    gs = GridSpec(num_rows, 2, figure=fig)
    
    # Convert time to pandas datetime for easy handling
    time_values = pd.to_datetime(ds["time"].values)

    # Plot the first variable, spanning the first row
    ax = fig.add_subplot(gs[0, :])
    variables[0].plot(ax=ax, color='k')
    ax.set_title(f"{variables[0].attrs.get('region', '')}")
    ax.set_xlim(np.min(time_values), np.max(time_values))
    ax.grid(color='#95a5a6', linestyle='-', alpha=0.25)

    # Define dataset-specific y-axis bounds
    if dataset_type == "error":  # If dataset is 'ds_err'
        lower_bound = 750  # Custom lower bound for errors
        upper_bound = 850    # Custom upper bound for errors
    else:  # Default dataset (ds)
        lower_bound = 250
        upper_bound = 1000

    # Identify large gaps and shade them
    for i in range(len(time_values) - 1):
        gap = (time_values[i + 1] - time_values[i]).days
        if gap > 35:
            ax.fill_between([time_values[i], time_values[i + 1]], 
                        max(ax.get_ylim()[0], upper_bound),  # Ensure reasonable lower bound
                        min(ax.get_ylim()[1], lower_bound),  # Ensure reasonable upper bound
                        color='gray', alpha=0.5)

    # Plot the remaining variables, two per row
    for i, da in enumerate(variables[1:], start=1):
        row = (i + 1) // 2
        col = (i + 1) % 2
        ax = fig.add_subplot(gs[row, col])
        da.plot(ax=ax, color='b', linewidth=1)
        ax.set_title(f"{da.attrs.get('region', '')}")
        ax.set_xlim(np.min(time_values), np.max(time_values))
        ax.grid(color='#95a5a6', linestyle='-', alpha=0.25)
        ax.tick_params(axis='x', rotation=45)

    plt.tight_layout()
    return fig, gs

With everything ready, let us now start with the analysis:

2. Quantifying Greenland Ice Sheet mass changes and their errors in space and time#

2.1 Time series of cumulative ice sheet mass changes#

We begin by plotting the GrIS cumulative mass change \(M_{GRACE}\) between the begin and end period with the defined plotting function, where the shading in the upper part of the plot indicates when the time between two consecutive measurements is more than 1 month:

Hide code cell source

 
fig, gs = plot_timeseries(ds)
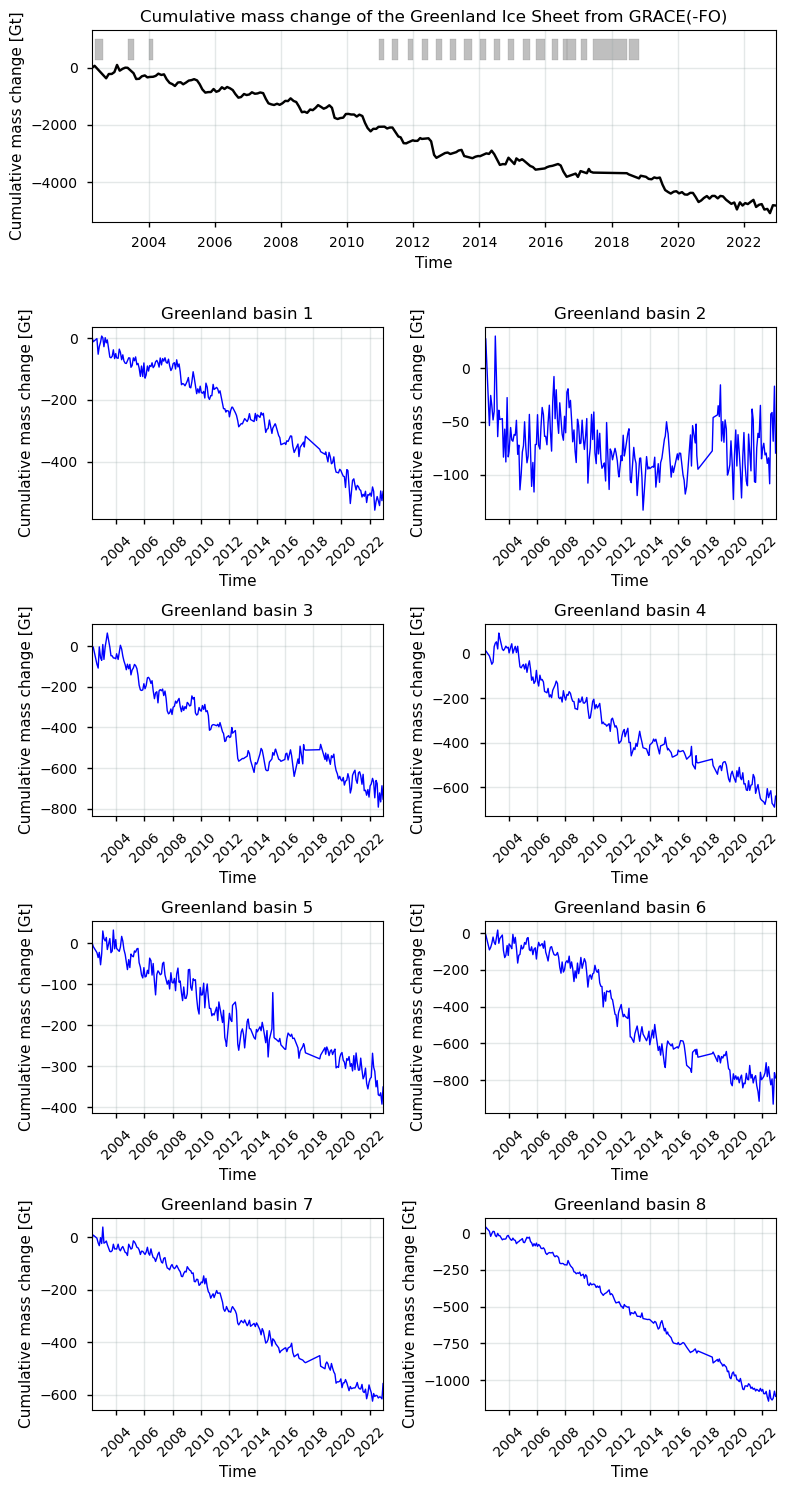
../../_images/6da32414e6b7e7ed1465d9c0cb485aa820cfa0999502fb64311fe2fd708541f5.png

Figure 1. Greenland ice sheet mass changes from GRACE(-FO). The top plot shows the mass changes over the entire ice sheet, where shaded intervals depict data gaps longer than 1 month. The smaller graphs below show the mass changes of the individual basins.

In the figure above, the first graph on top represents the cumulative mass change of the entire GrIS, while other graphs show the mass changes of its basins. Overall, these graphs depict a significant and widespread loss of ice mass across the practically the entire ice sheet, with different basins showing varying rates and patterns of ice loss. The findings underscore the critical state of the GrIS, serving as a clear indicator of the impacts of climate change [2, 4].

We recall the data are expressed as time series of cumulative values (mass anomalies) of the sum of mass changes driven by changing rates of solid ice discharge (i.e. the ice flux across the grounding line) and mass changes driven by changing rates of ablation and accumulation (mainly the SMB) at the basin-scale or ice sheet-wide scale.

2.2 Ice sheet mass changes uncertainty estimates#

The total error of a monthly ice sheet mass change estimate for Greenland is given by the sum of the precision (random) and the accuracy (systematic) error:

\( \varepsilon = a\sigma + \delta \) where \(a\) is the critical z-value related to a certain statistical confidence interval, \(\sigma\) is the standard deviation (random error) and \(\delta\) the accuracy (systematic) error.

For the GrIS, the product deals with both precision and accuracy errors in its final error estimates [5]. The precision error accounts for the statistically distributed random error around one average value. The accuracy error accounts for how much the expected value deviates from the “true” value, dervied from averaging mass change time series obtained with different methods, models and corrections. For the precision error, the 95% confidence interval (\(a\) = 1.96) propagated from the data, is provided. Therefore, in the case for the GrIS, the total uncertainty of the data is given by \(\varepsilon\). Hence, in the C3S products the most complete error estimate that was evaluated by Barletta et al. (2013) was given [5]. In the following section below, we will thus consider the uncertainty of the dataset as being \(\varepsilon_{M_{GRACE}}\).

Let us plot a time series of the errors:

Hide code cell source

 
fig, axs = plot_timeseries(ds_err, dataset_type="error")
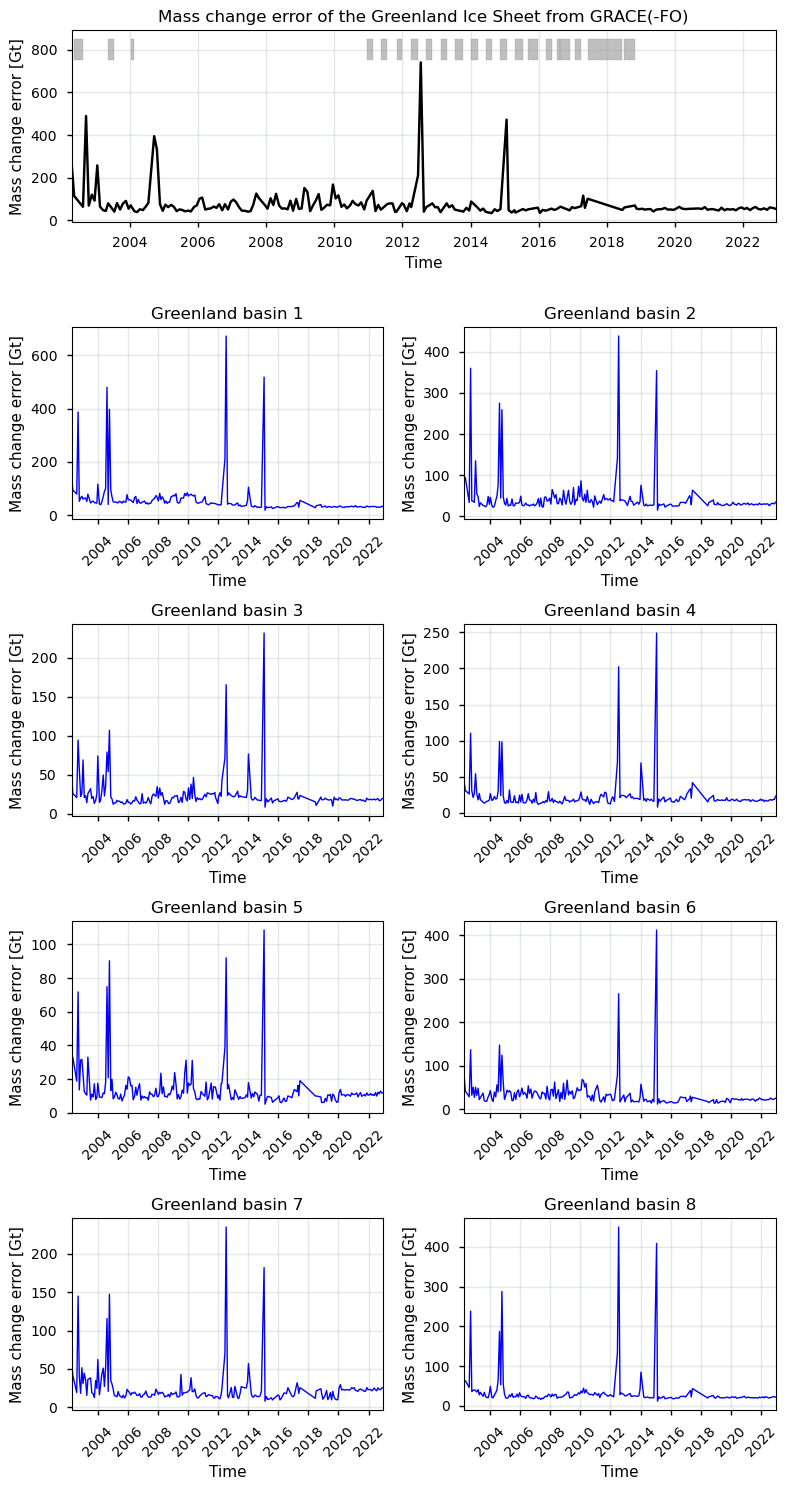
../../_images/e134041830e86c0db0844378d371e78cd0c57a7aae6d88aa8fd125cce7d0451d.png

Figure 2. Greenland ice sheet mass change errors from GRACE(-FO). The top plot shows the mass change errors over the entire ice sheet, where shaded intervals depict data gaps longer than 1 month. The smaller graphs below show the mass change errors of the individual basins.

Note that these values are not normalized to a certain time period, as the time gap between two measurements is (slightly) variable. Uncertainties in GRACE ice mass change estimates are occasionally very high and arise from various sources. These include, amongst others, errors related to measurement noise (e.g. due to leakage of the signal outside the region of interest such as the Canadian ice caps, due to the coarse resolution of GRACE(-FO) data acquisition), uncertainties related to the Earth’s gravitational field (e.g. due to the shift of the Earth’s center of mass, or due to the influence of the atmosphere and oceans on the Earth’s gravity field), and uncertainties related to other mass change signals that may be intertwined in the GRACE(-FO) data (e.g. those related to glacial isostatic adjustment).

We can furthermore calculate the average values (arithmetic means over time):

Hide code cell source

 
da = ds_err
variables = list(da.data_vars.values())
variables[0].attrs["region"] = f"in total"
for i, da in enumerate(variables, start=1):
    print(f"The arithmetic mean mass change error of the GrIS {da.attrs.get('region', '').replace('Greenland', '').strip()} is {np.mean(da.values):.2f} Gt with a maximum of {np.max(da.values):.2f} Gt.")

The arithmetic mean mass change error of the GrIS in total is 76.72 Gt with a maximum of 740.25 Gt.
The arithmetic mean mass change error of the GrIS basin 1 is 58.71 Gt with a maximum of 671.28 Gt.
The arithmetic mean mass change error of the GrIS basin 2 is 42.94 Gt with a maximum of 438.62 Gt.
The arithmetic mean mass change error of the GrIS basin 3 is 23.66 Gt with a maximum of 231.57 Gt.
The arithmetic mean mass change error of the GrIS basin 4 is 22.24 Gt with a maximum of 249.10 Gt.
The arithmetic mean mass change error of the GrIS basin 5 is 13.86 Gt with a maximum of 108.55 Gt.
The arithmetic mean mass change error of the GrIS basin 6 is 33.96 Gt with a maximum of 412.35 Gt.
The arithmetic mean mass change error of the GrIS basin 7 is 24.06 Gt with a maximum of 234.92 Gt.
The arithmetic mean mass change error of the GrIS basin 8 is 33.13 Gt with a maximum of 450.22 Gt.

For the entire ice sheet, error values mostly range between 50 and 100 gigatonnes (Gt), with occasional spikes reaching around 400 Gt or more. When comparing the errors to the respective mass change magnitudes, it can be noted that for the majority of the time series, the errors are relative large when compared to the actual changes in mass. This suggests that the data should be handled with care for most periods. The user can decide whether to leave the months with the highest errors out if desired. It is furthermore difficult to compare these errors to GCOS requirements (GCOS, 2022) because (a) the GCOS does not propose thresholds for mass change explicitely, but solely for ice sheet volume changes, (b) the GCOS reformulates error requirements in the form of precision errors (2\(\sigma\)), while the error in the GrIS mass change product contains an error product that combines precision and accuracy errors [5], and (c) the time difference between two GRACE measurements varies over time, and the time series also exhibits time gaps which complicates normalizing the errors to a common timeframe.

Concerning the errors, it must be said that in the C3S GrIS GMB products, the most complete error estimate that could be evaluated is included [5]. However, in contrast to other datasets, these errors are not easily formalized as the standard deviation or the 95% confidence interval. Most datasets namely do not usually provide the total error (i.e. they neglect the accuracy error). Apart all complex processes that can introduce uncertainty (as described above), this additionally provides a partial explanation for the relatively high uncertainty values for the ice sheet GMB dataset.

2.3 Application to an ice sheet modelling framework#

Let us now go back to our user question and assess whether the data are sufficiently adequate in terms of its spatio-temporal resolution and uncertainty to be applicable in glaciological modeling applications. Given the nature of the dataset and the above analysis, it is difficult to directly use GrIS (or AIS) GRACE(-FO) ice sheet mass change data into a “traditional” ice sheet model for several reasons:

  • Most importantly, ice sheet models that solve the continuity equation for prognostic ice thickness changes require surface mass balance (\(SMB\)) (and, if desired, basal mass balance (\(BMB\))) data (measured in m yr⁻¹ ice equivalents). However, GRACE(-FO) data include mass changes that combine both \(SMB\) and solid ice discharge (\(D\)) across the grounding line, complicating direct integration into models.

  • The coarse spatial resolution (actually, since no gridded data are provided, the term “spatial resolution” is not applicable for this dataset) and relatively high uncertainties of GRACE(-FO) data limit their ability to be useful in ice sheet models. GRACE(-FO) data are more suited for basin-scale or ice sheet-wide analyses rather than the fine-scale resolution (pixels or grid-based data) required for pixel-by-pixel modeling in ice sheet models.

To be directly usable in glaciological models, the C3S GRACE(-FO) GMB data would need a downscaling to higher spatial resolutions (i.e. reformatting into gridded products), an integration with SMB models or ice discharge data for component separation, and improved corrections/uncertainty characterization for certain months. The data can, however, be used for other purposes. GRACE(-FO) data are, for example, valuable for the direciton calculation and monitoring of ice sheet mass changes and their sea level contribution, or for the independent validation of ice sheet mass balance estimates from other methods. For example, they can help assess results from the input-output method, which quantifies the surface mass balance (\(SMB\)) and solid ice discharge (\(D\)) components seperately [6, 7], as well as for validating surface mass balance output from regional climate model outputs for Greenland (e.g. [7, 8, 9]). Studies, including Van den Broeke (2016) [9], have shown that cumulative surface mass balance (\(SMB\)) minus solid ice discharge (\(D\)) closely aligns with the trends and variability of GRACE(-FO) mass changes for Greenland, confirming the credibility and reliability of the GRACE(-FO) mass change data, despite the relatively high error/uncertainty values provided with the data.

3. Short summary and take-home messages#

The ice sheet mass change dataset, making use of the GRACE(-FO) satellite missions, is a useful tool for quantifying the total ice mass change of the Greenland (GrIS) Ice Sheet. It is one of the three main data acquisition methods that can extract ice mass change data from large spatial scales, such as the complete ice sheets, at a regular basis (the others being the altimetric and the input-output methods). The C3S ice sheet GMB data, with its long temporal extent (> 20 years), ice sheet-wide coverage and (quasi) monthly temporal resolution, effectively captures the long-term mean, trends and variability of ice sheet mass changes and the corresponding global sea level contributions. The data thus serve as a clear indicator of global climate change and water cycle changes.

Despite its strengths, GRACE(-FO) has certain limitations of which the user should take note, including a low spatial resolution (only ungridded ice-sheet-wide or basin-scale changes) and (occasionally very) high uncertainty values, including for example potential signal leakage from adjacent regions (e.g. the Canadian ice caps or peripheral glaciers and ice caps). Additional uncertainties furthermore arise from necessary geophysical corrections (e.g. glacial isostatic adjustment and intertwined mass changes from outer sources). Some GRACE(-FO) error values exhibit very high values, requiring careful interpretation. Additionally, data gaps (e.g. between the GRACE and GRACE-FO missions) affect the time series continuity, but these do not generally affect the overal trend and magnitude of the cumulative mass changes in the product (e.g. [10]). Nevertheless, unlike the input-output method (where SMB is directly needed) and the altimetric method (where it is necessary to obtain the firn density profiles for the volume-to-mass conversion), the SMB is not explicitly involved in the processing of GRACE(-FO) data, nor is it separated from ice flow dynamics. This independence negates uncertainties due to potential discrepancies between SMB model outputs from different centers and is a significant advantage of this method.

Moreover, due to the nature of the C3S GRACE(-FO) data presented on the CDS, they cannot be used directly as data assimilation into any glaciological model that requires the usage of pixel-based data to model ice thickness changes (e.g. an ice sheet model that solves the prognostic continuity equation on a grid). In essence, the results of this notebook therefore indicate that the product is inadequate to be used in most “traditional” glaciological modelling efforts because it is (1) only a spatially aggregated time series, (2) does not include SMB separately (which is to be used in the prognostic continuity equation for ice thickness changes), and (3) has high uncertainty in certain months. Nevertheless, it certainly has other applications and is highly relevant for the direct calculation and monitoring of ice sheet mass changes and their sea level contribution, and/or the validation of mass change estimates from other independent methods (e.g. the input-output method or the validation of the temporal variability of a surface mass balance model from a regional climate model) (e.g. [7, 8, 9]).

ℹ️ If you want to know more#

Key resources#

References#

  • [1] Forsberg, R., Sørensen, L.S. and Simonsen, S.B. (2017). Greenland and Antarctica Ice Sheet Mass Changes and Effects on Global Sea Level. Surv. Geophys., 38, 89–104. https://doi.org/10.1007/s10712-016-9398-7

  • [2] Groh, A., Horwath, M., Horvath, A., Meister, R., Sørensen, L.S., Barletta, V.R., Forsberg, R., Wouters, B., Ditmar, P., Ran, J., Klees, R., Su, X., Shang, K., Guo, J., Shum, C.K., Schrama, E., and Shepherd, A. (2019). Evaluating GRACE Mass Change Time Series for the Antarctic and Greenland Ice Sheet, Geosciences, 9(10). https://doi.org/10.3390/geosciences9100415

  • [3] Zwally, H., Giovinetto, M., Beckley, M., and Saba, J. (2012). Antarctic and Greenland drainage systems, GSFC cryospheric sciences laboratory. URL: https://earth.gsfc.nasa.gov/cryo/data/polar-altimetry/antarctic-and-greenland-drainage-systems

  • [4] Otosaka, I. N., Shepherd, A., Ivins, E. R., Schlegel, N.-J., Amory, C., van den Broeke, M. R., Horwath, M., Joughin, I., King, M. D., Krinner, G., Nowicki, S., Payne, A. J., Rignot, E., Scambos, T., Simon, K. M., Smith, B. E., Sørensen, L. S., Velicogna, I., Whitehouse, P. L., A, G., Agosta, C., Ahlstrøm, A. P., Blazquez, A., Colgan, W., Engdahl, M. E., Fettweis, X., Forsberg, R., Gallée, H., Gardner, A., Gilbert, L., Gourmelen, N., Groh, A., Gunter, B. C., Harig, C., Helm, V., Khan, S. A., Kittel, C., Konrad, H., Langen, P. L., Lecavalier, B. S., Liang, C.-C., Loomis, B. D., McMillan, M., Melini, D., Mernild, S. H., Mottram, R., Mouginot, J., Nilsson, J., Noël, B., Pattle, M. E., Peltier, W. R., Pie, N., Roca, M., Sasgen, I., Save, H. V., Seo, K.-W., Scheuchl, B., Schrama, E. J. O., Schröder, L., Simonsen, S. B., Slater, T., Spada, G., Sutterley, T. C., Vishwakarma, B. D., van Wessem, J. M., Wiese, D., van der Wal, W., and Wouters, B. (2023). Mass balance of the Greenland and Antarctic ice sheets from 1992 to 2020, Earth Syst. Sci. Data, 15, 1597–1616, https://doi.org/10.5194/essd-15-1597-2023

  • [5] Barletta, V. R., Sørensen, L. S., and Forsberg, R. (2013). Scatter of mass changes estimates at basin scale for Greenland and Antarctica, The Cryosphere, 7, 1411–1432, https://doi.org/10.5194/tc-7-1411-2013

  • [6] Mankoff, K. D., Solgaard, A., Colgan, W., Ahlstrøm, A. P., Khan, S. A., and Fausto, R. S. (2020). Greenland Ice Sheet solid ice discharge from 1986 through March 2020, Earth Syst. Sci. Data, 12, 1367–1383, https://doi.org/10.5194/essd-12-1367-2020

  • [7] Fettweis, X., Franco, B., Tedesco, M., van Angelen, J. H., Lenaerts, J. T. M., van den Broeke, M. R., and Gallée, H. (2013). Estimating the Greenland ice sheet surface mass balance contribution to future sea level rise using the regional atmospheric climate model MAR, The Cryosphere, 7, 469–489, https://doi.org/10.5194/tc-7-469-2013

  • [8] van den Broeke, M., Bamber, J., Ettema, J., Rignot, E., Schrama, E., van de Berg, W. J., van Meijgaard, E., Velicogna, I., and Wouters, B. (2009). Partitioning recent Greenland mass loss. Science, 326(5955), 984-986. https://doi.org/10.1126/science.1178176

  • [9] van den Broeke, M., Enderlin, E. M., Howat, I. M., Kuipers Munneke, P., Noël, B. P. Y., van de Berg, W. J., van Meijgaard, E., and Wouters, B. (2016). On the recent contribution of the Greenland ice sheet to sea level change, The Cryosphere, 10, 1933–1946, https://doi.org/10.5194/tc-10-1933-2016

  • [10] Velicogna, I., Mohajerani, Y., A, G., Landerer, F., Mouginot, J., Noel, B., Rignot, E., Sutterley, T., van den Broeke, M., van Wessem, M., and Wiese, D. (2020). Continuity of Ice Sheet Mass Loss in Greenland and Antarctica from the GRACE and GRACE Follow-On Missions. Geophys. Res. Lett. 47. https://doi.org/10.1029/2020GL087291

Contents